题目内容
(理)设F1,F2分别为椭圆W:
+
=1的左、右焦点,斜率为k(k>0)直线L经过右焦点F2,且与椭圆W相交于A,B两点.
(1)如果线段F2B的中点在y轴上,求直线l的方程;
(2)如果△ABF1为直角三角形,求直线l的斜率k.
| x2 |
| 6 |
| y2 |
| 2 |
(1)如果线段F2B的中点在y轴上,求直线l的方程;
(2)如果△ABF1为直角三角形,求直线l的斜率k.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)椭圆W的左焦点F1(-2,0),右焦点为F2(2,0),由已知条件得点B的横坐标为-2,点B的坐标为(-2,±
).由此能求出直线l的方程.
(2)由已知得∠BF1A=90°,∠BAF1=90°,或∠ABF1=90°.当∠BF1A=90°时,设直线AB的方程为y=k(x-2),A(x1,y1),B(x2,y2),由
,得(1+3k2)x2-12k2x+12k2-6=0,解得k=
;当∠BAF1=90°(与∠ABF1=90°相同)时,则点A在以线段F1F2为直径的圆x2+y2=4上,也在椭圆W上,
由
,解得A(
,1),或A(-
,1),或A(
,-1),或A(-
,-1),由此能求出直线l的斜率k=
,或k=2+
,或k=2-
时,△ABF1为直角三角形.
| ||
| 3 |
(2)由已知得∠BF1A=90°,∠BAF1=90°,或∠ABF1=90°.当∠BF1A=90°时,设直线AB的方程为y=k(x-2),A(x1,y1),B(x2,y2),由
|
| ||
| 23 |
由
|
| 3 |
| 3 |
| 3 |
| 3 |
| ||
| 23 |
| 3 |
| 3 |
解答:
(1)解:椭圆W的左焦点F1(-2,0),右焦点为F2(2,0),
因为线段F2B的中点在y轴上,
所以点B的横坐标为-2,
因为点B在椭圆W上,
将x=-2代入椭圆W的方程,得点B的坐标为(-2,±
).
所以直线AB(即l)的方程为x+2
y-2=0或x-2
-2=0.
(2)解:因为△ABF1为直角三角形,
所以∠BF1A=90°,∠BAF1=90°,或∠ABF1=90°.
当∠BF1A=90°时,
设直线AB的方程为y=k(x-2),A(x1,y1),B(x2,y2),
由
,得(1+3k2)x2-12k2x+12k2-6=0,
所以△=(12k2)2-4(1+3k2)(12k2-6)>0,
x1+x2=
,x1x2=
.
由∠BF1A=90°,得
•
=0,
因为
=(x1+2,y1),
=(x2+2,y2),
所以
•
=x1x2+2(x1+x2)+4+y1y2
=x1x2+2(x1+x2)+4+k2(x1-2)(x2-2)
=(1+k2)x1x2+(2-2k2)(x1+x2)+4+4k2
=(1+k2)×
+(2-2k2)×
+4+4k2=0,
解得k=±
(舍负).
当∠BAF1=90°(与∠ABF1=90°相同)时,
则点A在以线段F1F2为直径的圆x2+y2=4上,也在椭圆W上,
由
,
解得A(
,1),或A(-
,1),或A(
,-1),或A(-
,-1),
因为直线l的斜率为k>0,
所以由两点间斜率公式,得k=2+
,或k=2-
,
综上,直线l的斜率k=
,或k=2+
,或k=2-
时,△ABF1为直角三角形.
因为线段F2B的中点在y轴上,
所以点B的横坐标为-2,
因为点B在椭圆W上,
将x=-2代入椭圆W的方程,得点B的坐标为(-2,±
| ||
| 3 |
所以直线AB(即l)的方程为x+2
| 6 |
| 6 |
(2)解:因为△ABF1为直角三角形,
所以∠BF1A=90°,∠BAF1=90°,或∠ABF1=90°.
当∠BF1A=90°时,
设直线AB的方程为y=k(x-2),A(x1,y1),B(x2,y2),
由
|
所以△=(12k2)2-4(1+3k2)(12k2-6)>0,
x1+x2=
| 12k2 |
| 1+3k2 |
| 12k2-6 |
| 1+3k2 |
由∠BF1A=90°,得
| F1A |
| F1B |
因为
| F1A |
| F1B |
所以
| F1A |
| F1B |
=x1x2+2(x1+x2)+4+k2(x1-2)(x2-2)
=(1+k2)x1x2+(2-2k2)(x1+x2)+4+4k2
=(1+k2)×
| 12k2-6 |
| 1+3k2 |
| 12k2 |
| 1+3k2 |
解得k=±
| ||
| 23 |
当∠BAF1=90°(与∠ABF1=90°相同)时,
则点A在以线段F1F2为直径的圆x2+y2=4上,也在椭圆W上,
由
|
解得A(
| 3 |
| 3 |
| 3 |
| 3 |
因为直线l的斜率为k>0,
所以由两点间斜率公式,得k=2+
| 3 |
| 3 |
综上,直线l的斜率k=
| ||
| 23 |
| 3 |
| 3 |
点评:本题考查直线方程的求法,考查直线的斜率的求法,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
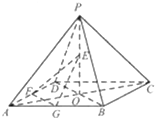 如图,四棱锤P-ABCD的底面为正方形,每题侧棱的长都等于底面的长,AC∩BD=O,E、F、G分别是PO、AD、AB的中点.
如图,四棱锤P-ABCD的底面为正方形,每题侧棱的长都等于底面的长,AC∩BD=O,E、F、G分别是PO、AD、AB的中点.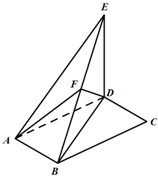 如图,平行四边形ABCD中,∠DAB=60°,AB=2,AD=4,将△CBD沿BD折起到△EBD的位置,使平面EBD⊥平面ABD.
如图,平行四边形ABCD中,∠DAB=60°,AB=2,AD=4,将△CBD沿BD折起到△EBD的位置,使平面EBD⊥平面ABD.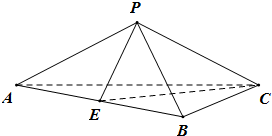 如图,在三棱锥P-ABC中,AB=2
如图,在三棱锥P-ABC中,AB=2