题目内容
已知函数f(x)=
(x∈R,a为常数),P1(x1,y1),P2(x2,y2)是函数y=f(x)图象上的两点.当线段P1P2的中点P的横坐标为
时,P的纵坐标恒为
.
(1)求y=f(x)的解析式;
(2)若数列{an}的通项公式为an=f(
)(n0∈N*,n=1,2,…,n),求数列{an}的前n0和Sn0.
| 1 |
| ax+2 |
| 1 |
| 2 |
| 1 |
| 4 |
(1)求y=f(x)的解析式;
(2)若数列{an}的通项公式为an=f(
| n |
| n0 |
考点:数列的求和
专题:点列、递归数列与数学归纳法
分析:(1)根据点P的坐标与函数之间的关系,即可求y=f(x)的解析式;
(2)求出数列的通项公式,利用构造方程即可得到结论.
(2)求出数列的通项公式,利用构造方程即可得到结论.
解答:
解:(1)由y=f(x)的图象上得y1=
,y2=
,
两式相加得
=
+
,化简得ax1+x2=4恒成立.
∵x1+x2=1,∴a=4,
∴f(x)=
.
(2)
=
(k=1,2,3,…,n0-1),
∴由已知条件得
=
,即f(
)+f(
)=
,
∴Sn=f(
)+f(
)+f(
)+…+f(
)+f(
),
∴Sn0=f(
)+f(
)+…+f(
)+f(
)+f(
)+f(
),两式相加得:
2Sn0=[f(
)+f(
)]+[f(
)+f(
)]+…+[f(
)+f(
)]+[f(
)+f(
)]+2f(
)
=
+
+…+
+2f(1)=
(n0-1)+2•
,
∴Sn0=
.
| 1 |
| ax1+2 |
| 1 |
| ax2+2 |
两式相加得
| 1 |
| 2 |
| 1 |
| ax1+2 |
| 1 |
| ax2+2 |
∵x1+x2=1,∴a=4,
∴f(x)=
| 1 |
| 4x+2 |
(2)
| ||||
| 2 |
| 1 |
| 2 |
∴由已知条件得
f(
| ||||
| 2 |
| 1 |
| 4 |
| k |
| n0 |
| n0-k |
| n0 |
| 1 |
| 2 |
∴Sn=f(
| 1 |
| n0 |
| 2 |
| n0 |
| 3 |
| n0 |
| n0-1 |
| n0 |
| n0 |
| n0 |
∴Sn0=f(
| n0-1 |
| n0 |
| n0-2 |
| n0 |
| 3 |
| n0 |
| 2 |
| n0 |
| 1 |
| n0 |
| n0 |
| n0 |
2Sn0=[f(
| 1 |
| n0 |
| n0-1 |
| n0 |
| 2 |
| n0 |
| n0-2 |
| n0 |
| n0-2 |
| n0 |
| 2 |
| n0 |
| n0-1 |
| n0 |
| 1 |
| n0 |
| n0 |
| n0 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 6 |
∴Sn0=
| 3n0-1 |
| 12 |
点评:本题主要考查函数解析式的求解以及数列求和的计算,综合性较强,运算量较大.

练习册系列答案
 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
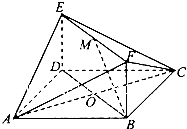 如图,已知正方形ABCD和矩形BDFE所在的平面互相垂直,AC交BD于O点,M为EF的中点,BC=
如图,已知正方形ABCD和矩形BDFE所在的平面互相垂直,AC交BD于O点,M为EF的中点,BC=