题目内容
设函数f(x)是定义在区间(-∞,+∞)上的偶函数,且满足f(1-x)=f(1+x)(x∈R).记Ik=(2k-1,2k+1](k∈Z).已知当x∈I°时,f(x)=x2.
(1)求函数f(x)的解析式;
(2)设k∈N*,Mk表示使方程f(x)=ax在x∈Ik上有两个不相等实根的a的取值集合.
①求M1;②求Mk.
(1)求函数f(x)的解析式;
(2)设k∈N*,Mk表示使方程f(x)=ax在x∈Ik上有两个不相等实根的a的取值集合.
①求M1;②求Mk.
考点:函数的零点与方程根的关系,函数解析式的求解及常用方法
专题:函数的性质及应用
分析:(1)由f(1-x)=f(1+x)?f(x+2)=f(-x)=f(x),得f(x)是以2为周x∈Ik期的函数,从而求出f(x)的解析式;
(2).①设x∈I1,则 x-2∈I0,得方程f(x)=ax可化为:x2-(4+a)x+4=0x∈(1,3](*)则:
;解出即可;
②当k∈N*且x∈Ik时,方程f(x)=ax化为x2-(4k+a)x+4k2=0,令g(x)=x2-(4k+a)x+4k2则
,解出即可.
(2).①设x∈I1,则 x-2∈I0,得方程f(x)=ax可化为:x2-(4+a)x+4=0x∈(1,3](*)则:
|
②当k∈N*且x∈Ik时,方程f(x)=ax化为x2-(4k+a)x+4k2=0,令g(x)=x2-(4k+a)x+4k2则
|
解答:
 解:(1)因为f(1-x)=f(1+x)?f(x+2)=f(-x)=f(x)
解:(1)因为f(1-x)=f(1+x)?f(x+2)=f(-x)=f(x)
所以 f(x)是以2为周x∈Ik期的函数,
∴f(x-2k)=f(x),(k∈Z),
当时,(x-2k)∈I°,
∴f(x)=f(x-2k)=(x-2k)2,
∴f(x)的解析式为:∴f(x)=(x-2k)2,x∈IK.
(2).①设x∈I1,则 x-2∈I0,∴f(x)=f(x-2)=(x-2)2,
方程f(x)=ax可化为:x2-(4+a)x+4=0x∈(1,3](*)
令g1(x)=x2-(4+a)x+4方程(*)在x∈(1,3]上有两相异实根,
则:
;
⇒a∈(0,
],∴M1=(0,
].
②当k∈N*且x∈Ik时,方程f(x)=ax化为x2-(4k+a)x+4k2=0,
令g(x)=x2-(4k+a)x+4k2…(10分)
使方程f(x)=ax在IK上有两个不相等的实数根,
则
,
即
,
∴0<a≤
,
∴MK={a|0<a≤
}.
 解:(1)因为f(1-x)=f(1+x)?f(x+2)=f(-x)=f(x)
解:(1)因为f(1-x)=f(1+x)?f(x+2)=f(-x)=f(x)所以 f(x)是以2为周x∈Ik期的函数,
∴f(x-2k)=f(x),(k∈Z),
当时,(x-2k)∈I°,
∴f(x)=f(x-2k)=(x-2k)2,
∴f(x)的解析式为:∴f(x)=(x-2k)2,x∈IK.
(2).①设x∈I1,则 x-2∈I0,∴f(x)=f(x-2)=(x-2)2,
方程f(x)=ax可化为:x2-(4+a)x+4=0x∈(1,3](*)
令g1(x)=x2-(4+a)x+4方程(*)在x∈(1,3]上有两相异实根,
则:
|
⇒a∈(0,
| 1 |
| 3 |
| 1 |
| 3 |
②当k∈N*且x∈Ik时,方程f(x)=ax化为x2-(4k+a)x+4k2=0,
令g(x)=x2-(4k+a)x+4k2…(10分)
使方程f(x)=ax在IK上有两个不相等的实数根,

则
|
即
|
∴0<a≤
| 1 |
| 2k+1 |
∴MK={a|0<a≤
| 1 |
| 2k+1 |
点评:本题考查了函数的零点和方程根的关系,考查函数的解析式的求法,本题属于中档题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
下列命题中,正确的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
两个平面能把空间分成几个部分( )
| A、2或3 | B、3或4 |
| C、3 | D、2或4 |
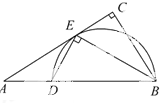 如图,在Rt△ABC中,∠=90°,BE平分∠ABC,交AC于点E,点D在AB上,DE⊥EB.
如图,在Rt△ABC中,∠=90°,BE平分∠ABC,交AC于点E,点D在AB上,DE⊥EB.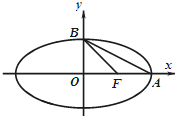 如图,椭圆C:
如图,椭圆C: