题目内容
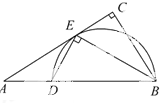 如图,在Rt△ABC中,∠=90°,BE平分∠ABC,交AC于点E,点D在AB上,DE⊥EB.
如图,在Rt△ABC中,∠=90°,BE平分∠ABC,交AC于点E,点D在AB上,DE⊥EB.(1)求证:AC是△BDE的外接圆的切线;
(2)若∠ABC=60°,AE=6,求EC的长.
考点:与圆有关的比例线段,圆的切线的判定定理的证明
专题:立体几何
分析:(1)设线段DB的中点为O,连结EO,由已知得OB=OE,∠OEB=∠OBE,∠CBE=∠OBE,∠OEB=∠CBE,OE∥BC,∠AEO=90°,由此能证明AC是△BDE的外切圆的切线.
(2)由C是圆O的切线,得∠OEA=90°,∠ABC=60°,OE∥BC,从而∠AOE=60°,OE=2
,由此能求出EC的长.
(2)由C是圆O的切线,得∠OEA=90°,∠ABC=60°,OE∥BC,从而∠AOE=60°,OE=2
| 3 |
解答:
(1)证明:设线段DB的中点为O,连结EO,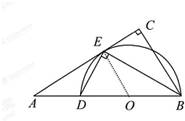
∵DE⊥EB,∴点O是圆心,∴OB=OE,
∴∠OEB=∠OBE,
又BE平分∠ABC,∴∠CBE=∠OBE,
∴∠OEB=∠CBE,∴OE∥BC,
又∵∠C=90°,∴∠AEO=90°,
∴AC是△BDE的外切圆的切线.
(2)解:由(1)知C是圆O的切线,
∠OEA=90°,∠ABC=60°,OE∥BC,
∴∠AOE=60°,∵AE=6,∴OE=2
,
△OBE中,∠OEB=∠OBE=30°,
∴BE=
OB=6,Rt△BEC中,∠OBE=30°,
∴CE=
BE=3.

∵DE⊥EB,∴点O是圆心,∴OB=OE,
∴∠OEB=∠OBE,
又BE平分∠ABC,∴∠CBE=∠OBE,
∴∠OEB=∠CBE,∴OE∥BC,
又∵∠C=90°,∴∠AEO=90°,
∴AC是△BDE的外切圆的切线.
(2)解:由(1)知C是圆O的切线,
∠OEA=90°,∠ABC=60°,OE∥BC,
∴∠AOE=60°,∵AE=6,∴OE=2
| 3 |
△OBE中,∠OEB=∠OBE=30°,
∴BE=
| 3 |
∴CE=
| 1 |
| 2 |
点评:本题考查三角形外接圆的切线的证明,考查线段长的求法,是中档题,解题时要认真审题,注意圆的性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
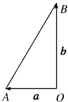
设
表示向西走10km,
表示向北走10
km,则
-
表示( )
| a |
| b |
| 3 |
| a |
| b |

| A、南偏西30°走20 km |
| B、北偏西30°走20 km |
| C、南偏东30°走20 km |
| D、北偏东30°走20 km |
某几何体的三视图如图所示,则该几何体的外接球的球面面积为( )
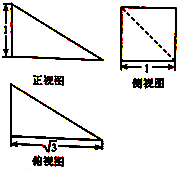

| A、5π | B、12π |
| C、20π | D、8π |
