题目内容

已知a∈（
2
，+∞），求
3a2-6
a2+1
的范围．
考点：函数的最值及其几何意义
专题：计算题,函数的性质及应用,不等式的解法及应用
分析：利用换元法令
3a2-6
=t，（t＞0）；从而化简故
3a2-6
a2+1
=
t
t2+6
3
+1
=
3t
t2+9
=
3
t+
9
t
，再利用基本不等式求解．
解答： 解：令
3a2-6
=t，（t＞0）；
则a2=
t2+6
3
；
故
3a2-6
a2+1
=
t
t2+6
3
+1
=
3t
t2+9

=
3
t+
9
t
，
∵t＞0，
∴t+
9
t
≥6；（当且仅当t=3时，等号成立）
∴0＜
3
t+
9
t
≤
1
2
．
故
3a2-6
a2+1
的取值范围为（0，
1
2
]．
点评：本题考查了换元法及基本不等式的应用，属于中档题．
练习册系列答案
相关题目
设抛物线W：y2=4x的焦点为F，过F的直线与W相交于A，B两点，记点F到直线l：x=-1的距离为d，则有（　　）
A、|AB|≥2d
B、|AB|=2d
C、|AB|≤2d
D、|AB|＜2d
函数f（x）=x3-x2+ax+b在点x=1处的切线与直线y=2x+1垂直，则a=
 
．
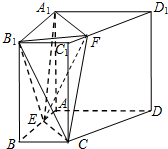如图，在四棱柱ABCD-A1B1C1D1中，A1A⊥底面ABCD，∠BAD=90°，AD∥BC，且A1A=AB=AD=2BC=2，点E在棱AB上，平面A1EC与棱C1D1相交于点F．
（Ⅰ）证明：A1F∥平面B1CE；
（Ⅱ）若E是棱AB的中点，求二面角A1-EC-D的余弦值；
（Ⅲ）求三棱锥B1-A1EF的体积的最大值．
已知椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）过点A（1，
3
2
），它的一个焦点是F（-1，0）．
（1）求椭圆的方程；
（2）P，Q是椭圆C上的两个动点，如果直线AP的倾斜角与AQ的倾斜角互补，证明：直线PQ定向（即该直线的斜率为定值）．
已知数列{an}的通项公式an=3n-2
（1）求（x-2y+3z） a3展开式中形如Ax4yzt的项的系数A；
（2）记bn=
1
3
（an+2），求证：（C
 
0
bn
）2+（C
 
1
bn
）2+（C
 
2
bn
）2+…+（C
 
bn
2bn
）2=C
 
bn
2bn
．
双曲线上右支上存在点P，使得右焦点F关于直线OP的对称点在y轴上（O为坐标原点），则双曲线离心率的取值范围为（　　）
A、(
2
，
3
)
B、(
2
，+∞)
C、(1，
2
)
D、(
3
，+∞)
在极坐标系中，点（3，
π
2
）到直线ρsin（θ-
π
4
）=2
2
的距离为
 
．
a
=（0，1），
b
=（1，0）且（
a
-
c
）•（
b
-
c
）=0，则|
c
|的最大值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网