Question

已知f（x）为定义在R上的偶函数，x≥0时，f（x）=x²-4x+3．
（1）求x＜0时函数的解析式；
（2）在给出的直角坐标系中画出y=f（x）的图象，并写出f（x）的单调递增区间；
（3）求函数f（x）在[0，3]的最大值及最小值．

Answer 1

考点：奇偶性与单调性的综合

专题：函数的性质及应用

分析：（1）利用偶函数的性质f（x）=f（-x）即可得出；
（2）利用二次函数的图象、偶函数的性质与单调性即可得出；
（3）函数f（x）在[0，2]上单调递减，在[2，3]单调递增．

解答： 解：（1）设x＜0，则-x＞0．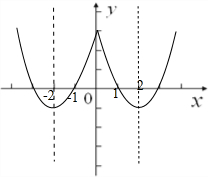
∵x≥0时，f（x）=x²-4x+3．
∴f（-x）=x²+4x+3．
∵f（x）为定义在R上的偶函数，
∴f（x）=f（-x））=x²+4x+3．
（2）y=f（x）的图象如图所示，
函数f（x）的单调递增区间为[-2，0]，[2，+∞）；
（3）函数f（x）在[0，2]上单调递减，在[2，3]单调递增．
而f（0）=3，f（2）=-1，f（3）=0．
∴函数f（x）在[0，3]的最大值为3，最小值-1．

点评：本题考查了二次函数的图象与性质、函数的奇偶性与单调性，考查了数形结合的能力，属于基础题．