题目内容
知直线ax+by+c=0与圆O:x2+y2=4相交于A、B二点,且|AB|=2
.
(1)求
•
的值;
(2)若直线AB过点(2,1),求直线AB的方程.
| 3 |
(1)求
| OA |
| OB |
(2)若直线AB过点(2,1),求直线AB的方程.
考点:平面向量数量积的运算
专题:平面向量及应用
分析:(1)首先求出OA,OB的夹角,按照向量的数量积的定义求之;
(2)利用点斜式方程,结合(1),利用点到直线的距离得到关于斜率的方程求k.
(2)利用点斜式方程,结合(1),利用点到直线的距离得到关于斜率的方程求k.
解答:
解:(1)由r=2,|AB|=2
⇒圆心到直线距离为1⇒∠AOB=120°⇒
•
=|
|•|
|cos120°=-2;
(2)设AB所在直线方程为y=k(x-2)+1即kx-y-2k+1=0,
由(1)可得
=1⇒k=0或k=
,
故所求直线方程:y=1或4x-3y-5=0.
| 3 |
| OA |
| OB |
| OA |
| OB |
(2)设AB所在直线方程为y=k(x-2)+1即kx-y-2k+1=0,
由(1)可得
| |2k-1| | ||
|
| 4 |
| 3 |
故所求直线方程:y=1或4x-3y-5=0.
点评:本题考查了向量的数量积的定义以及直线方程的求法,属于基础题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
某校为了了解1500名学生对学校食堂的意见,从中抽取1个容量为50的样本,采用系统抽样法,则分段间隔为( )
| A、10 | B、15 | C、20 | D、30 |
已知[x]表示不超过实数x的最大整数,例如[1.3]=1,[-2.6]=-3,g(x)=[x]为取整函数,已知x0是函数f(x)=lnx-
的零点,则g(x0)等于( )
| 2 |
| x |
| A、1 | B、2 | C、3 | D、4 |
下列各式中,值为0.5是( )
| A、sin15°cos15° | ||||||||
B、
| ||||||||
C、cos2
| ||||||||
D、
|
 已知f(x)为定义在R上的偶函数,x≥0时,f(x)=x2-4x+3.
已知f(x)为定义在R上的偶函数,x≥0时,f(x)=x2-4x+3.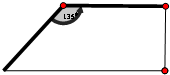 两直立矮墙成135°二面角,现利用这两面矮墙和篱笆围成一个面积为54m2的直角梯形菜园(墙足够长),已知修筑篱笆每米的费用为50元,则修筑这个菜园的最少费用为为
两直立矮墙成135°二面角,现利用这两面矮墙和篱笆围成一个面积为54m2的直角梯形菜园(墙足够长),已知修筑篱笆每米的费用为50元,则修筑这个菜园的最少费用为为