题目内容
2008年5月18日某爱心人士为一位孤儿去银行存款a元,存的是一年定期储蓄;2009年5月18日他将到期存款的本息一起取出,再加a元后,还存一年的定期储蓄,此后每年5月18日都如此;假设银行一年定期储蓄的年利率r不变,直到2015年5月18日这位孤儿准备上大学时,他将所有的存款和利息全部取出并且资助给这位孤儿,取出的钱数共为( )
| A、a(1+r)7元 | ||
| B、a[(1+r)7+(1+r)]元 | ||
C、
| ||
D、
|
考点:数列的应用
专题:点列、递归数列与数学归纳法
分析:根据题意,逐一求出2009年5月18日、2010年5月18日、2011年5月18日、2012年5月18日、2013年5月18日、2014年5月18日的存款,即可求出到2015年5月18日他将所有的存款和本息.
解答:
解:由题意,2009年5月18日的存款为a(1+r)+a元;
2010年5月18日的存款为a(1+r)2+a(1+r)+a元;
2011年5月18日的存款为a(1+r)3+a(1+r)2+a(1+r)+a元;
2012年5月18日的存款为a(1+r)4+a(1+r)3+a(1+r)2+a(1+r)+a元;
2013年5月18日的存款为a(1+r)5+a(1+r)4+a(1+r)3+a(1+r)2+a(1+r)+a元;
2014年5月18日的存款为a(1+r)6+a(1+r)5+a(1+r)4+a(1+r)3+a(1+r)2+a(1+r)+a元;
到2015年5月18日他所有的存款和本息为a(1+r)7+a(1+r)6+a(1+r)5+a(1+r)4+a(1+r)3+a(1+r)2+a(1+r)
=
[(1+r)8-(1+r)]元
故选D.
2010年5月18日的存款为a(1+r)2+a(1+r)+a元;
2011年5月18日的存款为a(1+r)3+a(1+r)2+a(1+r)+a元;
2012年5月18日的存款为a(1+r)4+a(1+r)3+a(1+r)2+a(1+r)+a元;
2013年5月18日的存款为a(1+r)5+a(1+r)4+a(1+r)3+a(1+r)2+a(1+r)+a元;
2014年5月18日的存款为a(1+r)6+a(1+r)5+a(1+r)4+a(1+r)3+a(1+r)2+a(1+r)+a元;
到2015年5月18日他所有的存款和本息为a(1+r)7+a(1+r)6+a(1+r)5+a(1+r)4+a(1+r)3+a(1+r)2+a(1+r)
=
| a |
| r |
故选D.
点评:本题以实际问题为载体,考查等比数列模型的构建,正确计算每年的存款是关键.

练习册系列答案
相关题目
若y=ax2+bx+c(a<0)中,两个零点x1<0,x2>0,且x1+x2>0,则( )
| A、b>0,c>0 |
| B、b>0,c<0 |
| C、b<0,c>0 |
| D、b<0,c<0 |
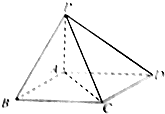 如图所示,在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥平面ABCD,且PA=AD=2,AB=1,AC=
如图所示,在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥平面ABCD,且PA=AD=2,AB=1,AC=