题目内容
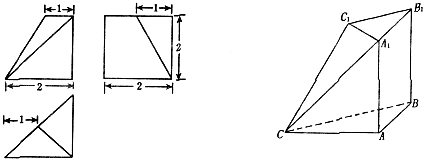
如图,多面体ABC-A1B1C1和它的三视图.
(1)线段CC1上是否存在一点E,使BE⊥平面A1CC1,若不存在请说明理由,若存在请找出并证明;
(2)求平面C1A1C与平面A1CA夹角的余弦值.
(1)线段CC1上是否存在一点E,使BE⊥平面A1CC1,若不存在请说明理由,若存在请找出并证明;
(2)求平面C1A1C与平面A1CA夹角的余弦值.

考点:直线与平面垂直的判定,二面角的平面角及求法
专题:证明题,空间位置关系与距离,空间角
分析:(1)由题意知AA1,AB,AC两两垂直,建立空间直角坐标系,设存在一点E,使BE⊥平面A1CC1,设
=λ
,由此利用向量法能求出线段CC1上存在一点E,满足
=2
,使BE⊥平面A1CC1.
(2)求出平面C1A1C的法向量和平面A1CA的一个法向量,利用向量法能求出平面C1A1C与平面A1CA夹角余弦值.
| CE |
| EC1 |
| CE |
| EC1 |
(2)求出平面C1A1C的法向量和平面A1CA的一个法向量,利用向量法能求出平面C1A1C与平面A1CA夹角余弦值.
解答:
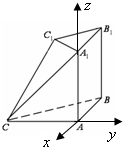 证明:(1)由已知知AA1,AB,AC两两垂直,如图建系,BC=2
证明:(1)由已知知AA1,AB,AC两两垂直,如图建系,BC=2
,则A(0,0,0),
A1(0,0,2),B(-2,0,0),C(0,-2,0),C1(-1,-1,2),
=(-1,1,2)
=(-1,-1,0),
=(0,-2,-2).…(1分)
设E(x,y,z),则
=(x,y+2,z)
=(-1-x,-1-y,2-z)…(3分)
设
=λ
,⇒
则E(
,
,
),
=(
,
,
)…(4分)
由
⇒
,得λ=2
所以线段CC1上存在一点E,
=2
,使BE⊥平面A1CC1…(6分)
另证:补形成正方体,易证CE:EC1=2:1
(2)设平面A1C1C的法向量为
=(x,y,z),则由
,得
,
取x=1,则y=-1,z=1.故
=(1,-1,1),…(8分)
而平面A1AC的一个法向量为
=(1,0,0),则cos<
,
>=
=
=
…(11分)
平面C1A1C与平面A1CA夹角的余弦值为
…(12分)
 证明:(1)由已知知AA1,AB,AC两两垂直,如图建系,BC=2
证明:(1)由已知知AA1,AB,AC两两垂直,如图建系,BC=2| 2 |
A1(0,0,2),B(-2,0,0),C(0,-2,0),C1(-1,-1,2),
| CC1 |
| A1C1 |
| A1C |
设E(x,y,z),则
| CE |
|
设
| CE |
| EC1 |
|
则E(
| -λ |
| 1+λ |
| -2-λ |
| 1+λ |
| 2λ |
| 1+λ |
| BE |
| 2+λ |
| 1+λ |
| -2-λ |
| 1+λ |
| 2λ |
| 1+λ |
由
|
|
所以线段CC1上存在一点E,
| CE |
| EC1 |
另证:补形成正方体,易证CE:EC1=2:1
(2)设平面A1C1C的法向量为
| m |
|
|
取x=1,则y=-1,z=1.故
| m |
而平面A1AC的一个法向量为
| n |
| m |
| n |
| ||||
|
|
| 1 | ||
|
| ||
| 3 |
平面C1A1C与平面A1CA夹角的余弦值为
| ||
| 3 |
点评:本题考查直线与平面平行的证明,考查直线与平面垂直的证明,考查平面与平面的夹角的余弦值的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
函数f(x)=2x3-6x的“临界点”是( )
| A、1 | B、-1 | C、-1和1 | D、0 |
如图,在△OAB中,P为线段AB上的一点,
=x
+y
,且
=3
,则( )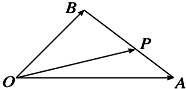
| OP |
| OA |
| OB |
| BP |
| PA |

A、x=
| ||||
B、x=
| ||||
C、x=
| ||||
D、x=
|
2008年5月18日某爱心人士为一位孤儿去银行存款a元,存的是一年定期储蓄;2009年5月18日他将到期存款的本息一起取出,再加a元后,还存一年的定期储蓄,此后每年5月18日都如此;假设银行一年定期储蓄的年利率r不变,直到2015年5月18日这位孤儿准备上大学时,他将所有的存款和利息全部取出并且资助给这位孤儿,取出的钱数共为( )
| A、a(1+r)7元 | ||
| B、a[(1+r)7+(1+r)]元 | ||
C、
| ||
D、
|
一几何体的正视图和侧视图是边长为2的等边三角形,俯视图是直径为2的圆,则此几何体的表面积为( )

A、4π+2
| ||
B、2π+2
| ||
| C、3π | ||
| D、2π |

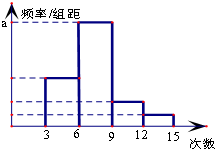 对某校高二年级学生参加社区服务次数进行统计,随机抽取N名学生作为样本,得到这N名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如图:
对某校高二年级学生参加社区服务次数进行统计,随机抽取N名学生作为样本,得到这N名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如图: