题目内容
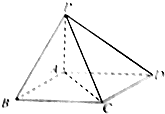 如图所示,在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥平面ABCD,且PA=AD=2,AB=1,AC=
如图所示,在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥平面ABCD,且PA=AD=2,AB=1,AC=| 3 |
(1)证明:CD⊥平面PAC;
(2)求四棱锥P-ABCD的体积.
考点:直线与平面垂直的判定,棱柱、棱锥、棱台的体积
专题:证明题,空间位置关系与距离
分析:(1)由PA⊥平面ABCD,CD?平面ABCD可证明PA⊥CD,在△ACD中,由已知可得AC2+CD2=AD2,即CD⊥AC,又PA∩AC=A,PA?平面PAC,AC?平面PAC,从而证明CD⊥平面PAC.
(2)先求S四边形ABCD=AB×AC=
,从而由VP-ABCD=
×S四边形ABCD×PA,即可求解.
(2)先求S四边形ABCD=AB×AC=
| 3 |
| 1 |
| 3 |
解答:
(本小题满分12分)
解:(1)证明:∵PA⊥平面ABCD,CD?平面ABCD
∴PA⊥CD…(2分)
在△ACD中,AD=2,CD=1,AC=
,
∴AC2+CD2=AD2
∴∠ACD=90°,即CD⊥AC…(4分)
又PA∩AC=A,PA?平面PAC,AC?平面PAC,
∴CD⊥平面PAC…(6分)
(2)∵S四边形ABCD=AB×AC=
…(9分)
∴VP-ABCD=
×S四边形ABCD×PA=
×
×2=
…(12分)
解:(1)证明:∵PA⊥平面ABCD,CD?平面ABCD
∴PA⊥CD…(2分)
在△ACD中,AD=2,CD=1,AC=
| 3 |
∴AC2+CD2=AD2
∴∠ACD=90°,即CD⊥AC…(4分)
又PA∩AC=A,PA?平面PAC,AC?平面PAC,
∴CD⊥平面PAC…(6分)
(2)∵S四边形ABCD=AB×AC=
| 3 |
∴VP-ABCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
2
| ||
| 3 |
点评:本题主要考查了直线与平面垂直的判定,考查了棱柱、棱锥、棱台的体积的解法,体现了数形结合和等价转化的数学思想,属于中档题.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
 已知函数f(x)=
已知函数f(x)=
|
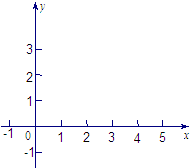
(1)在如图所示给定的直角坐标系内画出f(x)的图象;
(2)写出f(x)的单调递增区间;
(3)由图象指出当x取什么值时f(x)有最值.
2008年5月18日某爱心人士为一位孤儿去银行存款a元,存的是一年定期储蓄;2009年5月18日他将到期存款的本息一起取出,再加a元后,还存一年的定期储蓄,此后每年5月18日都如此;假设银行一年定期储蓄的年利率r不变,直到2015年5月18日这位孤儿准备上大学时,他将所有的存款和利息全部取出并且资助给这位孤儿,取出的钱数共为( )
| A、a(1+r)7元 | ||
| B、a[(1+r)7+(1+r)]元 | ||
C、
| ||
D、
|
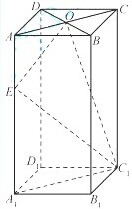 如图,长方体ABCD-A1B1C1D1中,底面A1B1C1D1是正方形,E为棱AA1上任意一点,F是CD的中点.
如图,长方体ABCD-A1B1C1D1中,底面A1B1C1D1是正方形,E为棱AA1上任意一点,F是CD的中点.