题目内容
用长度为24m、的材料围一个矩形场地，中间有两道隔墙，要使矩形的面积最大，则隔墙的长度应为多少？为什么？
考点：基本不等式在最值问题中的应用
专题：应用题,函数的性质及应用
分析：若设矩形场地的宽为x，则长为
，其面积为S=
•x，整理得x的二次函数，能求出函数的最值以及对应的x的值．
| 24-4x |
| 2 |
| 24-4x |
| 2 |
解答：
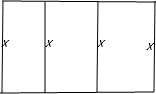解：如图所示，设矩形场地的宽为x，则长为
，其面积为：
S=
•x=12x-2x2=-2（x2-6x+9）+18=-2（x-3）2+18
当x=3时，S有最大值，为18；
所以隔墙宽应为3．
解：如图所示，设矩形场地的宽为x，则长为| 24-4x |
| 2 |
S=
| 24-4x |
| 2 |
当x=3时，S有最大值，为18；
所以隔墙宽应为3．
点评：本题借助于矩形的周长与面积，考查了二次函数的最值问题，是基础题目．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
2008年5月18日某爱心人士为一位孤儿去银行存款a元，存的是一年定期储蓄；2009年5月18日他将到期存款的本息一起取出，再加a元后，还存一年的定期储蓄，此后每年5月18日都如此；假设银行一年定期储蓄的年利率r不变，直到2015年5月18日这位孤儿准备上大学时，他将所有的存款和利息全部取出并且资助给这位孤儿，取出的钱数共为（ ）
| A、a（1+r）7元 | ||
| B、a[（1+r）7+（1+r）]元 | ||
C、
| ||
D、
|
一几何体的正视图和侧视图是边长为2的等边三角形，俯视图是直径为2的圆，则此几何体的表面积为（ ）
A、4π+2
| ||
B、2π+2
| ||
| C、3π | ||
| D、2π |
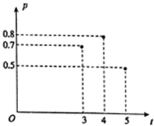加工爆米花时，爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”，在特定条件下，可食用率p与加工时间t（单位：分钟）满足下列某函数关系：①p=at+b②p=alogbt③p=at2+bt+c（a，b，c是常数），如图记录了三次实验的数据，