题目内容
已知f(x)=asin(πx+α)+bcos(πx+β)+4(a,b,α,β为非零实数),f(2013)=5,求f(0)+f(1)+…+f(2014)的值.
考点:数列的求和,函数的周期性
专题:等差数列与等比数列
分析:由f(2013)=5,可得-asinα-bcosβ+4=5,即asinα+bcosβ=-1,可得f(0)=asinα+bcosβ+4=3,f(1)=-asinα-bcosβ+4=5,f(2)=asinα+bcosβ+4=3,f(3)=-asinα-bcosβ+4=5,…,即可得出.
解答:
解:∵f(2013)=5,
∴asin(2013π+α)+bcos(2013π+β)+4=5,
化为-asinα-bcosβ+4=5,
∴asinα+bcosβ=-1,
∵f(0)=asinα+bcosβ+4=3,
f(1)=-asinα-bcosβ+4=5,
f(2)=asinα+bcosβ+4=3,
f(3)=-asinα-bcosβ+4=5,
…,
∴f(0)+f(1)+…+f(2014)
=[f(0)+f(2)+…+f(2014)]+[f(1)+f(3)+…+f(2013)]
=1008×3+1007×5
=8059.
∴asin(2013π+α)+bcos(2013π+β)+4=5,
化为-asinα-bcosβ+4=5,
∴asinα+bcosβ=-1,
∵f(0)=asinα+bcosβ+4=3,
f(1)=-asinα-bcosβ+4=5,
f(2)=asinα+bcosβ+4=3,
f(3)=-asinα-bcosβ+4=5,
…,
∴f(0)+f(1)+…+f(2014)
=[f(0)+f(2)+…+f(2014)]+[f(1)+f(3)+…+f(2013)]
=1008×3+1007×5
=8059.
点评:本题考查了函数的奇偶性、分类讨论方法、分组数列求和、诱导公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
2008年5月18日某爱心人士为一位孤儿去银行存款a元,存的是一年定期储蓄;2009年5月18日他将到期存款的本息一起取出,再加a元后,还存一年的定期储蓄,此后每年5月18日都如此;假设银行一年定期储蓄的年利率r不变,直到2015年5月18日这位孤儿准备上大学时,他将所有的存款和利息全部取出并且资助给这位孤儿,取出的钱数共为( )
| A、a(1+r)7元 | ||
| B、a[(1+r)7+(1+r)]元 | ||
C、
| ||
D、
|
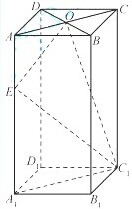 如图,长方体ABCD-A1B1C1D1中,底面A1B1C1D1是正方形,E为棱AA1上任意一点,F是CD的中点.
如图,长方体ABCD-A1B1C1D1中,底面A1B1C1D1是正方形,E为棱AA1上任意一点,F是CD的中点.