题目内容
已知函数f(x)=
sin2x+2cosx•sin(x-
)+sinxcosx.
(1)求函数y=f(x)的增区间
(2)若2f(x)-m+1=0在[
,
]有两个相异的实根,求m的取值范围.
| 3 |
| π |
| 3 |
(1)求函数y=f(x)的增区间
(2)若2f(x)-m+1=0在[
| π |
| 6 |
| 7π |
| 12 |
考点:三角函数中的恒等变换应用,正弦函数的图象
专题:三角函数的图像与性质
分析:(1)由三角函数中的恒等变换应用化简函数解析式可得f(x)=2sin(2x-
),由-
+2kπ≤2x-
≤
+2kπ,即可解得函数y=f(x)的增区间.
(2)由已知转化为方程f(x)=
两个相异的实根,即y=f(x)图象与y=
图象有两个交点,结合函数图象,有1≤
<2,即可解得m的取值范围.
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
(2)由已知转化为方程f(x)=
| m-1 |
| 2 |
| m-1 |
| 2 |
| m-1 |
| 2 |
解答:
解:(1)∵f(x)=
sin2x+2cosx•sin(x-
)+sinxcosx…2分
=
×(
)+2cosx(
sinx-
cosx)+sinxcosx
=sin2x-
cos2x
=2sin(2x-
)…4分
∴由-
+2kπ≤2x-
≤
+2kπ,得-
+kπ≤x≤
+kπ(k∈Z)…6分
(2)2f(x)-m+1=0在[
,
]内有两个相异的实根,
f(x)=
两个相异的实根,
即y=f(x)图象与y=
图象有两个交点,…8分
结合函数图象,当1≤
<2,
解得:m∈[3,5)时原方程有两个相异的实根,
故m∈[3,5)…13分
| 3 |
| π |
| 3 |
=
| 3 |
| 1-cos2x |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
=sin2x-
| 3 |
=2sin(2x-
| π |
| 3 |
∴由-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| π |
| 12 |
| 5π |
| 12 |
(2)2f(x)-m+1=0在[
| π |
| 6 |
| 7π |
| 12 |
f(x)=
| m-1 |
| 2 |
即y=f(x)图象与y=
| m-1 |
| 2 |
结合函数图象,当1≤
| m-1 |
| 2 |
解得:m∈[3,5)时原方程有两个相异的实根,
故m∈[3,5)…13分
点评:本题主要考查了三角函数中的恒等变换应用,正弦函数的图象和性质的应用,考查了转化思想,属于中档题.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
如图,在△OAB中,P为线段AB上的一点,
=x
+y
,且
=3
,则( )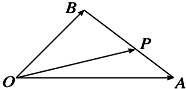
| OP |
| OA |
| OB |
| BP |
| PA |

A、x=
| ||||
B、x=
| ||||
C、x=
| ||||
D、x=
|
2008年5月18日某爱心人士为一位孤儿去银行存款a元,存的是一年定期储蓄;2009年5月18日他将到期存款的本息一起取出,再加a元后,还存一年的定期储蓄,此后每年5月18日都如此;假设银行一年定期储蓄的年利率r不变,直到2015年5月18日这位孤儿准备上大学时,他将所有的存款和利息全部取出并且资助给这位孤儿,取出的钱数共为( )
| A、a(1+r)7元 | ||
| B、a[(1+r)7+(1+r)]元 | ||
C、
| ||
D、
|
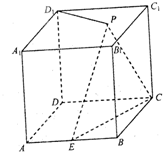 在棱长为2的正方体ABCD-A1B1C1D1中,E为棱AB的中点,点P在平面A1B1C1D1内,若D1P⊥平面PCE,试求线段D1P的长.
在棱长为2的正方体ABCD-A1B1C1D1中,E为棱AB的中点,点P在平面A1B1C1D1内,若D1P⊥平面PCE,试求线段D1P的长.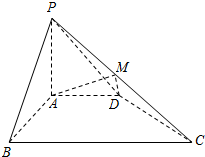 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=AD=2,四边形AB⊥CD,BC∥AD且BC=4,点M为PC中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=AD=2,四边形AB⊥CD,BC∥AD且BC=4,点M为PC中点.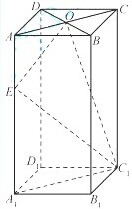 如图,长方体ABCD-A1B1C1D1中,底面A1B1C1D1是正方形,E为棱AA1上任意一点,F是CD的中点.
如图,长方体ABCD-A1B1C1D1中,底面A1B1C1D1是正方形,E为棱AA1上任意一点,F是CD的中点.