题目内容
小辉是一位收藏爱好者,在第1年初购买了价值为20万元的收藏品M,由于受到收藏品市场行情的影响,第2年、第3年的每年初M的价值为上年初的
;从第4年开始,每年初M的价值比上年初增加4万元.
(Ⅰ)求第几年初开始M的价值超过原购买的价值;
(Ⅱ)记Tn(n∈N*)表示收藏品M前n年的价值的平均值,求Tn的最小值.
| 1 |
| 2 |
(Ⅰ)求第几年初开始M的价值超过原购买的价值;
(Ⅱ)记Tn(n∈N*)表示收藏品M前n年的价值的平均值,求Tn的最小值.
考点:数列的应用
专题:点列、递归数列与数学归纳法
分析:(Ⅰ)根据题意,写成通项公式,计算即可;
(Ⅱ)分1≤n≤3及n≥4两种情况分析即可.
(Ⅱ)分1≤n≤3及n≥4两种情况分析即可.
解答:
解:(Ⅰ)设第n年初M的价值为an,
依题意,当1≤n≤3时,数列{an}是首项为20,公比为
的等比数列,
所以an=20×(
)n-1=5×23-n.故a2=10,a3=5,所以a3<a2<a1.
当n≥4时,数列{an}是以a4为首项,公差为4的等差数列,
又a4=a3+4=9,所以an=9+(n-4)×4=4n-7.
令an>20,得n>
,又因为n∈N*,所以n≥7.
因此,第7年初M开始的价值an超过原购买的价值.
(Ⅱ)设Sn表示前n年初M的价值的和,则Tn=
由(Ⅰ)知,当1≤n≤3时,Sn=
=40-5×23-n,
Tn=
①;
当n≥4时,由于S3=35,故Sn=S3+(a4+a5+…+an)=35+
=2n2-5n+32,
Tn=
=2n+
-5.②
当1≤n≤3时,由①得,T1=20,T2=15,T3=
,所以T1>T2>T3
当n≥4时,由②知,Tn=2n+
-5 ≥ 2
-5=11,
当且仅当2n=
,即n=4时等号成立.即(Tn)min=T4=11.
由于T3>T4,故在第4年初Tn的值最小,其最小值为11.
依题意,当1≤n≤3时,数列{an}是首项为20,公比为
| 1 |
| 2 |
所以an=20×(
| 1 |
| 2 |
当n≥4时,数列{an}是以a4为首项,公差为4的等差数列,
又a4=a3+4=9,所以an=9+(n-4)×4=4n-7.
令an>20,得n>
| 27 |
| 4 |
因此,第7年初M开始的价值an超过原购买的价值.
(Ⅱ)设Sn表示前n年初M的价值的和,则Tn=
| Sn |
| n |
由(Ⅰ)知,当1≤n≤3时,Sn=
20•(1-(
| ||
1-
|
Tn=
| 40-5×23-n |
| n |
当n≥4时,由于S3=35,故Sn=S3+(a4+a5+…+an)=35+
| (n-3)(9+4n-7) |
| 2 |
Tn=
| 2n2-5n+32 |
| n |
| 32 |
| n |
当1≤n≤3时,由①得,T1=20,T2=15,T3=
| 35 |
| 3 |
当n≥4时,由②知,Tn=2n+
| 32 |
| n |
2n•
|
当且仅当2n=
| 32 |
| n |
由于T3>T4,故在第4年初Tn的值最小,其最小值为11.
点评:本小题主要考查数列、等差数列、等比数列、不等式等基础知识,考查运算求解能力、抽象概括能力、应用意识,考查函数与方程思想、化归与转化思想、分类与整合思想.

练习册系列答案
相关题目
已知椭圆的方程为x2+
=1(0<a<1),椭圆上离顶点A(0,a)的最远点为(0,-a),则实数a的取值范围是( )
| y2 |
| a2 |
| A、0<a<1 | ||||
B、
| ||||
C、
| ||||
D、0<a<
|
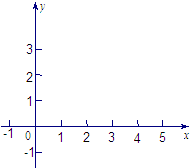 已知函数f(x)=
已知函数f(x)=
|
(1)在如图所示给定的直角坐标系内画出f(x)的图象;
(2)写出f(x)的单调递增区间;
(3)由图象指出当x取什么值时f(x)有最值.
2008年5月18日某爱心人士为一位孤儿去银行存款a元,存的是一年定期储蓄;2009年5月18日他将到期存款的本息一起取出,再加a元后,还存一年的定期储蓄,此后每年5月18日都如此;假设银行一年定期储蓄的年利率r不变,直到2015年5月18日这位孤儿准备上大学时,他将所有的存款和利息全部取出并且资助给这位孤儿,取出的钱数共为( )
| A、a(1+r)7元 | ||
| B、a[(1+r)7+(1+r)]元 | ||
C、
| ||
D、
|
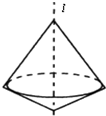 要得到如图所示的几何体,只需将图所示的三角形绕直线l旋转一周,则可以是( )
要得到如图所示的几何体,只需将图所示的三角形绕直线l旋转一周,则可以是( )