题目内容
（理科）解不等式：x2+（a-1）x-a≥0．
考点：一元二次不等式的解法
专题：分类讨论,不等式的解法及应用
分析：把不等式化为（x+a）（x-1）≥0，讨论a的取值，得出对应不等式的解集．
解答：
解：原不等式可化为（x+a）（x-1）≥0；
∴当a＞-1时，不等式的解集为{x|x≤-a或x≥1}；
当a=-1时，不等式的解集为R；
当a＜-1时，不等式的解集为{x|x≤1或x≥-a}．
∴当a＞-1时，不等式的解集为{x|x≤-a或x≥1}；
当a=-1时，不等式的解集为R；
当a＜-1时，不等式的解集为{x|x≤1或x≥-a}．
点评：本题考查了解含有字母系数的一元二次不等式的问题，解题时应利用分类讨论的方法进行解答，是基础题．
练习册系列答案
学而优衔接教材南京大学出版社系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
将4名学生分到三个不同的班级，在每个班级至少分到一名学生的条件下，其中甲、乙两名学生不能分到同一个班级的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
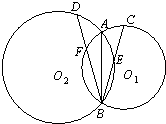如图，假设两圆O1和O2交于A、B，⊙O1的弦BC交⊙O2于E，⊙O2的弦BD交⊙O1于F，证明：