题目内容
设数列{an}满足:a1=3,an+l=3an,n∈N*.
(Ⅰ)求{an}的第4项a4及前5项和S5;
(Ⅱ)设数列{bn}满足:b1=1,bn-1=
,Tn=b1+b2•3+b3•32+…+bn•3n-1,证明:数列{4Tn-3n•bn}为等差数列.
(Ⅰ)求{an}的第4项a4及前5项和S5;
(Ⅱ)设数列{bn}满足:b1=1,bn-1=
| 1 |
| an-1 |
考点:数列递推式,等差关系的确定
专题:等差数列与等比数列
分析:(Ⅰ)根据条件得到数列{an}为等比数列,即可得到结论;
(Ⅱ)根据等差数列的定义,即可得到结论.
(Ⅱ)根据等差数列的定义,即可得到结论.
解答:
解:(Ⅰ)因为an+l=3an,又a1=3,所以
=3,
因此{an}是首项为3,公比为3的等比数列,
所以an=3n,a4=34,=81,Sn=
=
(3n-1),S5=
(35-1)=363.
(Ⅱ)证明:Tn=b1+b2•3+b3•32+…+bn•3n-1,①
Tn-1=b1+b2•3+b3•32+…+bn-1•3n-2,②
Tn-Tn-1=bn•3n-1,
所以4Tn-3n•bn-(4Tn-1-3n-1•bn-1)=4•3n-1•bn-3•3n-1•bn+•3n-1•bn-1
=•3n-1•bn+•3n-1•bn-1=•3n-1•(bn+bn-1)=1,
所以,数列{4Tn-3n•bn}为等差数列.
| an+1 |
| an |
因此{an}是首项为3,公比为3的等比数列,
所以an=3n,a4=34,=81,Sn=
| 3(1-3n) |
| 1-3 |
| 3 |
| 2 |
| 3 |
| 2 |
(Ⅱ)证明:Tn=b1+b2•3+b3•32+…+bn•3n-1,①
Tn-1=b1+b2•3+b3•32+…+bn-1•3n-2,②
Tn-Tn-1=bn•3n-1,
所以4Tn-3n•bn-(4Tn-1-3n-1•bn-1)=4•3n-1•bn-3•3n-1•bn+•3n-1•bn-1
=•3n-1•bn+•3n-1•bn-1=•3n-1•(bn+bn-1)=1,
所以,数列{4Tn-3n•bn}为等差数列.
点评:本题主要考查等差数列和等比数列的判断,考查学生的计算能力.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
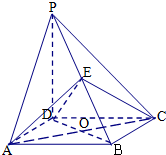 如图四棱锥P-ABCD中,底面ABCD是正方形,PD⊥底面ABCD,点E在棱PB上.
如图四棱锥P-ABCD中,底面ABCD是正方形,PD⊥底面ABCD,点E在棱PB上.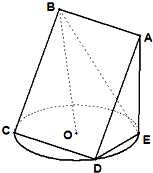 如图,正方形ABCD所在平面与圆O所在平面相交于CD,线段CD为圆O的弦,AE垂直于圆O所在平面,垂足E是圆O上异于C、D的点,AE=3,正方形的边长为3
如图,正方形ABCD所在平面与圆O所在平面相交于CD,线段CD为圆O的弦,AE垂直于圆O所在平面,垂足E是圆O上异于C、D的点,AE=3,正方形的边长为3 如图所示,已知圆O的直径AB=
如图所示,已知圆O的直径AB=