题目内容
判断函数f（x）=
+
的奇偶性．
| 1-x2 |
| x2-1 |
考点：函数奇偶性的判断
专题：计算题,函数的性质及应用
分析：先求函数定义域，观察是否关于原点对称，然后运用定义判断．
解答：
解：由
，得x=±1，
∴函数的定义域为{-1，1}，关于原点对称，
则f（x）=0，
f（-x）=f（x）=0，f（-x）=-f（x）=0，
∴f（x）既是奇函数又是偶函数．
|
∴函数的定义域为{-1，1}，关于原点对称，
则f（x）=0，
f（-x）=f（x）=0，f（-x）=-f（x）=0，
∴f（x）既是奇函数又是偶函数．
点评：本题考查函数奇偶性的判断，属基础题．注意定义域关于原点对称是函数具备奇偶性的必要不充分条件．
练习册系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
第三学期赢在暑假系列答案
相关题目
在△ABC中，A，B，C所对边分别为a，b，c，则下列各式中一定成立的是（ ）
A、
| ||||
B、
| ||||
| C、asinB=bcosA | ||||
| D、a=2RcosA |
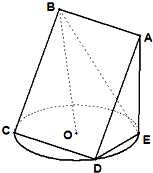如图，正方形ABCD所在平面与圆O所在平面相交于CD，线段CD为圆O的弦，AE垂直于圆O所在平面，垂足E是圆O上异于C、D的点，AE=3，正方形的边长为3