Question

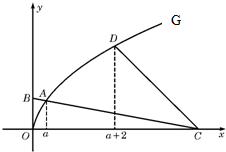如图，曲线G的方程为y=

2x

．直线BC与曲线G交于点A，设B（0，b），C（c，0），点A的横坐标为a，当|

.

OA

|=|

.

OB

|时，
（Ⅰ）求点A的横坐标a与点C的横坐标c的关系式；
（Ⅱ）设曲线G上点D的横坐标为a+2，求直线CD的倾斜角．

Answer 1

考点：直线的一般式方程

专题：直线与圆

分析：（I）利用两点之间的距离公式、直线的截距式即可得出；
（II）利用斜率计算公式即可得出．

解答： 解：（Ⅰ）由题意知，A(a，

2a

)．
∵|OA|=t，∴a²+2a=t²．
由于t＞0，故有t=

a2+2a

．　（1）
由点B（0，t），C（c，0）的坐标知，
直线BC的方程为

x

c

+

y

t

=1．
又因点A在直线BC上，故有

a

c

+

2a

t

=1，
将（1）代入上式，得

a

c

+

2a

a(a+2)

=1，
解得c=a+2+

2(a+2)

．
（Ⅱ）∵D(a+2，

2(a+2)

)，
∴直线CD的斜率为k_CD=

2(a+2)

a+2-c

=

2(a+2)

a+2-(a+2+ 2(a+2) )

=

2(a+2)

- 2(a+2)

=-1．
∴直线CD的倾斜角为135°．

点评：本题考查了两点之间的距离公式、直线的截距式、斜率与倾斜角的关系及其计算公式，考查了计算能力，属于中档题．