题目内容
| C | 1 2n |
| C | 3 2n |
| C | 5 2n |
| C | 2n-1 2n |
考点:二项式系数的性质
专题:二项式定理
分析:直接利用二项式定理系数的性质求解即可.
解答:
解:由(a+b)2n=C2n0a2nb0+C2n1•a2n-1b1+C2n2•a2n-2•b2+…+C2n2n•a0•b2n,
系数的性质,奇数项系数的和等于偶数项系数的和,
∴
+
+
+…+
=22n.
故答案为:22n
系数的性质,奇数项系数的和等于偶数项系数的和,
∴
| C | 1 2n |
| C | 3 2n |
| C | 5 2n |
| C | 2n-1 2n |
故答案为:22n
点评:本题考查二项式定理系数的性质,注意奇数项系数的和与偶数项系数和相等是解题的关键,考查计算能力.

练习册系列答案
相关题目
已知等差数列{an}前n项和为Sn,若a1+a2012=1,a2013=-1006,则使Sn取最值时n的值为( )
| A、1005 |
| B、1006 |
| C、1007 |
| D、1006或1007 |
“m>3”是“方程
-
=1表示双曲线”的( )
| x2 |
| m-1 |
| y2 |
| m-3 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
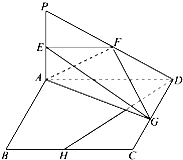 如图所示,PA⊥平面ABCD,四边形ABCD为正方形,且AD=2PA,E,F,G,H分别是线段PA,PD,CD,BC的中点.
如图所示,PA⊥平面ABCD,四边形ABCD为正方形,且AD=2PA,E,F,G,H分别是线段PA,PD,CD,BC的中点.