题目内容
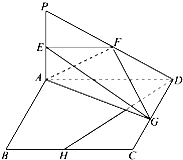 如图所示,PA⊥平面ABCD,四边形ABCD为正方形,且AD=2PA,E,F,G,H分别是线段PA,PD,CD,BC的中点.
如图所示,PA⊥平面ABCD,四边形ABCD为正方形,且AD=2PA,E,F,G,H分别是线段PA,PD,CD,BC的中点.(Ⅰ)求证:平面FDH⊥平面AEG;
(Ⅱ)求三棱锥E-AFG与四棱锥P-ABCD的体积比.
考点:棱柱、棱锥、棱台的体积,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(Ⅰ)由已知得AE⊥DH,DH⊥AG,从而DH⊥平面AEG,由此能证明平面FDH⊥平面AEG.
(Ⅱ)
=
,由此能求出结果.
(Ⅱ)
| VE-AFG |
| VP-ABCD |
| VG-AEF |
| VP-ABCD |
解答:
(Ⅰ)证明:∵PA⊥平面ABCD,
∴PA⊥DH,即AE⊥DH,
∵△ADG≌△DCH,∴∠HDC=∠DAG,∠AGD+∠DAG=90°.
∴∠AGD+∠HDC=90°.∴DH⊥AG.
又∵AE∩AG=A,∴DH⊥平面AEG
又∵DH?平面DHF,∴平面FDH⊥平面AEG.…(6分)
(Ⅱ)解:
=
=
…(9分)
=
=
=
.…(12分)
∴PA⊥DH,即AE⊥DH,
∵△ADG≌△DCH,∴∠HDC=∠DAG,∠AGD+∠DAG=90°.
∴∠AGD+∠HDC=90°.∴DH⊥AG.
又∵AE∩AG=A,∴DH⊥平面AEG
又∵DH?平面DHF,∴平面FDH⊥平面AEG.…(6分)
(Ⅱ)解:
| VE-AFG |
| VP-ABCD |
| VG-AEF |
| VP-ABCD |
=
| ||
|
=
| ||||
| PA×AD×CD |
=
| ||||||||
| PA×AD×CD |
=
| 1 |
| 16 |
点评:本题考查平面与平面垂直的证明,考查两个几何体的体积之比的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
设等边△ABC边长为6,若
=3
,
=
,则
•
等于( )
| BC |
| BE |
| AD |
| DC |
| BD |
| AE |
A、-6
| ||
B、6
| ||
| C、-18 | ||
| D、18 |
如图所示,在四面体A-BCD中,若截面PQMN是正方形,则在下列命题中错误的为( )
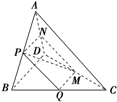

| A、AC⊥BD |
| B、AC∥截面PQMN |
| C、AC=BD |
| D、BD∥截面PQMN |