题目内容
12.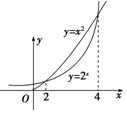 已知当x≥0时,函数y=x2与函数y=2x的图象如图所示,则当x≤0时,不等式2x•x2≥1的解集是[-4,-2].
已知当x≥0时,函数y=x2与函数y=2x的图象如图所示,则当x≤0时,不等式2x•x2≥1的解集是[-4,-2].
分析 在不等式2x•x2≥1 中,令x=-t.由x≤0得t≥0,故不等式即 2-t•t2≥1,即 t2≥2t,由所给图象得2≤t≤4,由此求得x的范围.
解答 解:根据当x≥0时,函数y=x2与函数y=2x的图象如图,可得当x=2,或x=4时,x2 =2x,
且在[2,4]上,x2 ≥2x .
当x≤0时,令x=-t,由x≤0得t≥0,∴不等式2x•x2≥1,即 2-t•t2≥1,即 t2≥2t.
由所给图象得2≤t≤4,即-2≤-x≤4,求得-4≤x≤-2,
故答案为:[-4,-2].
点评 本题主要考查函数的图象和性质应用,属于中档题.

练习册系列答案
相关题目
2.在△ABC中,若$\overrightarrow{AB}•\overrightarrow{AC}=|\overrightarrow{AB}-\overrightarrow{AC}|=8$,则△ABC的面积的最大值为( )
| A. | 8 | B. | 16 | C. | $10\sqrt{3}$ | D. | $8\sqrt{6}$ |
3.已知函数f(x)=2x3-6x2+3,则函数f(x)在[-2,2]上的最小值为( )
| A. | -37 | B. | -29 | C. | -5 | D. | 以上都不对 |
20.从装有两个红球和两个黑球的口袋里任取两个球,那么对立的两个事件是( )
| A. | “至少有一个黑球”与“都是黑球” | |
| B. | “至少有一个黑球”与“至少有一个红球” | |
| C. | “恰好有一个黑球”与“恰好有两个黑球” | |
| D. | “至少有一个黑球”与“都是红球” |
2.若$a={2^x},b={log_{\frac{1}{2}}}x$则“x>1”是“a>b”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |