题目内容
1.已知f(α)=$\frac{{sin({α-π})cos({2π-α})sin({α+\frac{π}{2}})}}{{cos({π+α})sin({π-α})}}$.(Ⅰ) 化简f(α);
(Ⅱ)求f(α)的对称轴方程及单调递增区间.
分析 (Ⅰ) 利用诱导公式化简即可;
(Ⅱ)根据三角函数的性质求解对称轴方程及单调递增区间.
解答 解:(Ⅰ)f(α)=$\frac{{sin({α-π})cos({2π-α})sin({α+\frac{π}{2}})}}{{cos({π+α})sin({π-α})}}$=$\frac{(-sinα)•cosα•cosα}{(-cosα)•sinα}$=cosα.
(Ⅱ)∵f(α)=cosα,
根据余弦函数的性质可得:
对称轴方程α=kπ,k∈Z.
单调递增区间为[-π+2kπ,2kπ].
点评 本题主要考察了诱导公式的化解能力和余弦函数的性质,属于基本知识的考查.

练习册系列答案
相关题目
11.若实数a,b,c∈(0,1)且10a+9b=9,a+b+c=1,则当$\frac{10}{a}+\frac{1}{9b}$取最小值时,c的值为( )
| A. | $\frac{5}{11}$ | B. | $\frac{2}{11}$ | C. | $\frac{1}{11}$ | D. | 0 |
9.在下列各数中,最大的数是( )
| A. | 85(9) | B. | 11111(2) | C. | 68(8) | D. | 210(6) |
16.设${\vec e}_1,{\vec e}_2$是两个单位向量,则下列结论正确的是( )
| A. | ${\vec e}_1={\vec e}_2$ | B. | ${\vec e}_1∥{\vec e}_2$ | C. | $|{{\vec e}_1}|=|{{\vec e}_2}|$ | D. | 以上都不对 |
11.若a,b,c∈R,且$a={x^2}-2y+\frac{π}{2},b={y^2}-2z+\frac{π}{3},c={z^2}-2x+\frac{π}{6}$,则下列说法正确的是( )
| A. | a,b,c都大于0 | B. | a,b,c中至少有一个大于0 | ||
| C. | a,b,c都小于0 | D. | a,b,c中至多有一个大于0 |
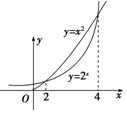 已知当x≥0时,函数y=x2与函数y=2x的图象如图所示,则当x≤0时,不等式2x•x2≥1的解集是[-4,-2].
已知当x≥0时,函数y=x2与函数y=2x的图象如图所示,则当x≤0时,不等式2x•x2≥1的解集是[-4,-2].