题目内容
7.直线l经过点A(3,-1),且在第四象限与两坐标轴围成等腰三角形,则直线l的方程为x-y-4=0.分析 设直线l的方程为y+1=k(x-3),k>0,根据题意在第四象限与两坐标轴围成等腰三角形,可得$\frac{1}{k}$+3=3k+1,由此求得k的值,可得直线l的方程.
解答 解:∵直线l经过点A(3,-1),设直线l的方程为y+1=k(x-3),k>0,
则直线和x轴的交点为($\frac{1}{k}$+3,0),和y轴的交点为( 0,-3k-1 ),
根据题意可得$\frac{1}{k}$+3=3k+1,即3k2-2k-1=0,求得k=1,或k=-$\frac{1}{3}$(舍去),
故直线l的方程为 y+1=1(x-3),即 x-y-4=0,
故答案为:x-y-4=0.
点评 本题主要考查直线得点斜式方程,用待定系数法求直线的方程,属于基础题.

练习册系列答案
相关题目
15.设集合M={x2-2x<0},N={x|x≤1},则M∩N=( )
| A. | (0,1) | B. | (1,2) | C. | (0,2) | D. | (0,1] |
2.利用独立性检测来考查两个分类变量X,Y是否有关系,当随机变量K2的值( )
| A. | 越大,“X与Y有关系”成立的可能性越大 | |
| B. | 越大,“X与Y有关系”成立的可能性越小 | |
| C. | 越小,“X与Y有关系”成立的可能性越大 | |
| D. | 与“X与Y有关系”成立的可能性无关 |
19.已知z=(m-1)+mi为纯虚数,则在复平面内,复数z=2-mi对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
16.设${\vec e}_1,{\vec e}_2$是两个单位向量,则下列结论正确的是( )
| A. | ${\vec e}_1={\vec e}_2$ | B. | ${\vec e}_1∥{\vec e}_2$ | C. | $|{{\vec e}_1}|=|{{\vec e}_2}|$ | D. | 以上都不对 |
 如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC=1,O为AC的中点,PO⊥平面ABCD,M为PD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC=1,O为AC的中点,PO⊥平面ABCD,M为PD的中点.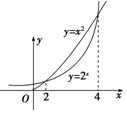 已知当x≥0时,函数y=x2与函数y=2x的图象如图所示,则当x≤0时,不等式2x•x2≥1的解集是[-4,-2].
已知当x≥0时,函数y=x2与函数y=2x的图象如图所示,则当x≤0时,不等式2x•x2≥1的解集是[-4,-2].