题目内容
4.(-i)2017+(1+i)2=i.分析 (-i)4=1,可得(-i)2017=[(-i)4]504•(-i)=-i.即可得出.
解答 解:∵(-i)4=1,可得(-i)2017=[(-i)4]504•(-i)=-i.
∴原式=-i+2i=i.
故答案为:i.
点评 本题考查了复数的运算法则、周期性,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
15.设集合M={x2-2x<0},N={x|x≤1},则M∩N=( )
| A. | (0,1) | B. | (1,2) | C. | (0,2) | D. | (0,1] |
19.已知z=(m-1)+mi为纯虚数,则在复平面内,复数z=2-mi对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
9.在下列各数中,最大的数是( )
| A. | 85(9) | B. | 11111(2) | C. | 68(8) | D. | 210(6) |
16.设${\vec e}_1,{\vec e}_2$是两个单位向量,则下列结论正确的是( )
| A. | ${\vec e}_1={\vec e}_2$ | B. | ${\vec e}_1∥{\vec e}_2$ | C. | $|{{\vec e}_1}|=|{{\vec e}_2}|$ | D. | 以上都不对 |
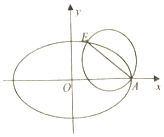 如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的右顶点为A,离心率为e,且椭圆C过点$E({2e,\frac{b}{2}})$,以AE为直径的圆恰好经过椭圆的右焦点.
如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的右顶点为A,离心率为e,且椭圆C过点$E({2e,\frac{b}{2}})$,以AE为直径的圆恰好经过椭圆的右焦点.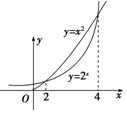 已知当x≥0时,函数y=x2与函数y=2x的图象如图所示,则当x≤0时,不等式2x•x2≥1的解集是[-4,-2].
已知当x≥0时,函数y=x2与函数y=2x的图象如图所示,则当x≤0时,不等式2x•x2≥1的解集是[-4,-2].