题目内容
20.从装有两个红球和两个黑球的口袋里任取两个球,那么对立的两个事件是( )| A. | “至少有一个黑球”与“都是黑球” | |
| B. | “至少有一个黑球”与“至少有一个红球” | |
| C. | “恰好有一个黑球”与“恰好有两个黑球” | |
| D. | “至少有一个黑球”与“都是红球” |
分析 根据题意,由互斥事件与对立事件的定义,依次分析选项,即可得答案.
解答 解:根据题意,依次分析四个选项:
对于A、“都是黑球”是“至少有一个黑球”的一种情况,不是对立事件,
对于B、“至少有一个黑球”包括“2个都是黑球”和“一红一黑”两种情况,而“至少有一个红球”包括“2个都是红球”和“一红一黑”两种情况,
两者不是对立事件,
对于C、“恰好有一个黑球”即“一红一黑”,与“恰好有两个黑球”是互斥事件,但不是对应事件,
对于D、“至少有一个黑球”包括“2个都是黑球”和“一红一黑”两种情况,与都是红球”为对立事件;
故选:D.
点评 本题考查互斥事件与对立事件的定义,其中关键是熟练掌握互斥事件与对立事件的定义.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
11.若实数a,b,c∈(0,1)且10a+9b=9,a+b+c=1,则当$\frac{10}{a}+\frac{1}{9b}$取最小值时,c的值为( )
| A. | $\frac{5}{11}$ | B. | $\frac{2}{11}$ | C. | $\frac{1}{11}$ | D. | 0 |
8.为调查某地区老人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)请根据上面的数据分析该地区的老年人需要志愿者提供帮助与性别有关吗?
| 性别 是否需要志愿者 | 男 | 女 |
| 需要 | 40 | 30 |
| 不需要 | 160 | 270 |
(2)请根据上面的数据分析该地区的老年人需要志愿者提供帮助与性别有关吗?
15.设集合M={x2-2x<0},N={x|x≤1},则M∩N=( )
| A. | (0,1) | B. | (1,2) | C. | (0,2) | D. | (0,1] |
5.在调查男女乘客是否晕机的情况中,已知男乘客晕机为28人,不会晕机的也是28人,而女乘客晕机为28人,不会晕机的为56人.
(1)根据以上数据完成右边 2×2列联表;
(2)试判断晕机是否与性别有关?
(参考数据:K2≥2.706时,有90%的把握判定变量A,B有关联;K2≥3.841时,有95%的把握判定变量A,B有关联;K2≥6.635时,有99%的把握判定变量A,B有关联.参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+c)(b+d)(a+b)(c+d)}$)
| 晕机 | 不晕机 | 总计 | |
| 男乘客 | |||
| 女乘客 | |||
| 总计 |
(2)试判断晕机是否与性别有关?
(参考数据:K2≥2.706时,有90%的把握判定变量A,B有关联;K2≥3.841时,有95%的把握判定变量A,B有关联;K2≥6.635时,有99%的把握判定变量A,B有关联.参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+c)(b+d)(a+b)(c+d)}$)
9.在下列各数中,最大的数是( )
| A. | 85(9) | B. | 11111(2) | C. | 68(8) | D. | 210(6) |
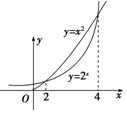 已知当x≥0时,函数y=x2与函数y=2x的图象如图所示,则当x≤0时,不等式2x•x2≥1的解集是[-4,-2].
已知当x≥0时,函数y=x2与函数y=2x的图象如图所示,则当x≤0时,不等式2x•x2≥1的解集是[-4,-2].