题目内容
17.用0,1,2,3,4,5这六个数字组成无重复数字的正整数.(1)共有多少个四位数?
(2)其中四位偶数有多少个?
(3)比4301大的四位数有多少个?
(4))能组成多少个无重复数字且为5的倍数的五位数?
(注意:以上各小题要列出算式后再求值,否则扣分.)
分析 (1)先安排首位的数字,从五个非0数字中选一个,共有C51种结果,余下的五个数字在三个位置进行全排列,共有A53种结果,根据乘法原理得到结果.
(2)要组成无重复数字的四位偶数,则末位为0,2,4中一个,且首位不能为0,所以可用分类计数,分成三类,0在个位,2在个位,4在个位,把每类的方法数计算出来,再相加即可.
(3)当首位是5时,其他几个数字在三个位置上排列,当首位是4时,第二位是5.后两位没有限制,当前两位是43时,分别写出结果数(注意减去4301),相加得到结果.
(4)要组成无重复数字的5的倍数的五位数,则末位为0,5中一个,且首位不能为0,所以可用分类计数,分成两类,0在个位,5在个位,把每类的方法数计算出来,再相加即可
解答 解:(1)由题意知,因为数字中有0,0不能放在首位,
∴先安排首位的数字,从五个非0数字中选一个,共有C51种结果,
余下的五个数字在三个位置进行全排列,共有A53种结果,
根据分步计数原理知共有A15•A35=300;
(2)第一类:0在个位时有A53个;第二类:2在个位时,首位从1,3,4,5中选定1个(有A41种),十位和百位从余下的数字中选(有A42种),于是有A41A42个;第三类:4在个位时,与第二类同理,也有A41A42个.
共有四位偶数:A53+A41A42+A41A42=156个.
(3)当首位是5时,其他几个数字在三个位置上排列,共有A53=60,
当前两位是45时,共有A43=4×3=12个,
当前两位是43时,共有A42=4×3=12个,去掉4301即可,即有12-1=11个.
根据分类加法原理得到共有:60+12+12-1=83个.
(4)个位数上的数字是0的五位数有A54个;个位数上的数字是5的五位数有A41A43个.
故满足条件的五位数的个数共有A54+A41A43=216个.
点评 本题是考查排列组合问题,是一个综合题,包括数字问题中可能遇到的所有情况,同学们注意分析问题,加以比较,争取做到举一反三.

| A. | -2 | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
| 性别 是否需要志愿者 | 男 | 女 |
| 需要 | 40 | 30 |
| 不需要 | 160 | 270 |
(2)请根据上面的数据分析该地区的老年人需要志愿者提供帮助与性别有关吗?
| 晕机 | 不晕机 | 总计 | |
| 男乘客 | |||
| 女乘客 | |||
| 总计 |
(2)试判断晕机是否与性别有关?
(参考数据:K2≥2.706时,有90%的把握判定变量A,B有关联;K2≥3.841时,有95%的把握判定变量A,B有关联;K2≥6.635时,有99%的把握判定变量A,B有关联.参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+c)(b+d)(a+b)(c+d)}$)
| A. | 恰好有两个解 | B. | 至少有一个解 | C. | 至少有两个解 | D. | 至少有三个解 |
| A. | 85(9) | B. | 11111(2) | C. | 68(8) | D. | 210(6) |
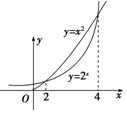 已知当x≥0时,函数y=x2与函数y=2x的图象如图所示,则当x≤0时,不等式2x•x2≥1的解集是[-4,-2].
已知当x≥0时,函数y=x2与函数y=2x的图象如图所示,则当x≤0时,不等式2x•x2≥1的解集是[-4,-2].