题目内容
一条光线从原点(0,0)射到直线l:2x-y+5=0上,再经反射后过B(1,3),求反射光线所在直线的方程.
考点:与直线关于点、直线对称的直线方程
专题:直线与圆
分析:设出(0,0)关于直线2x-y+5=0对称的点,由两点的中点在直线l上,且两点连线的斜率与直线l的斜率互为负倒数联立方程组求得对称点的坐标,然后求出反射光线的斜率,由直线方程的点斜式得答案.
解答:
解:设(0,0)关于直线2x-y+5=0对称的点为(x0,y0),
则
=-
…①,
2•
-
+5=0…②,
①②联立解得
.
∴(0,0)关于直线2x-y+5=0对称的点坐标为(-4,2).
∴反射光线所在直线的斜率k=
=
,
方程为:y-3=
(x-1),整理:x-5y+14=0.
则
| y0 |
| x0 |
| 1 |
| 2 |
2•
| x0 |
| 2 |
| y0 |
| 2 |
①②联立解得
|
∴(0,0)关于直线2x-y+5=0对称的点坐标为(-4,2).
∴反射光线所在直线的斜率k=
| 3-2 |
| 1-(-4) |
| 1 |
| 5 |
方程为:y-3=
| 1 |
| 5 |
点评:本题考查了点关于直线的对称点的求法,考查了直线的点斜式方程,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
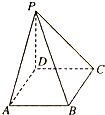 如图所示,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,PD⊥底面ABCD,且PD=a,PA=PC=
如图所示,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,PD⊥底面ABCD,且PD=a,PA=PC=| 2 |
(1)求证:点A在PA为直径的圆上;
(2)若在这个四棱锥内放一球,求此球的最大半径.
已知正四面体ABCD的棱长为1,则
•
=(( )
| AB |
| CD |
A、-
| ||
B、
| ||
| C、1 | ||
| D、0 |
正三棱锥的三视图如图所示,则其外接球的体积为( )
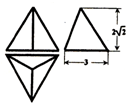

A、9
| ||||
B、
| ||||
| C、18π | ||||
| D、6π |
设函数f(x)可导,则
=( )
| lim |
| △x→0 |
| f(1+△x)-f(1) |
| △x |
| A、f′(1) |
| B、f′(x) |
| C、-f′(1) |
| D、-f′(x) |
下列等式成立的是( )
| A、(cos2x)'=sin2x | ||||
B、
| ||||
C、
| ||||
| D、(3x)'=x•3x-1 |
若函数f(x)=logax(a>0且a≠0)在[4,16]上的最大值比最小值大1,则实数a的值为( )
A、
| ||
B、
| ||
| C、4 | ||
| D、以上都不对 |