题目内容

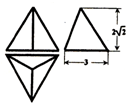
正三棱锥的三视图如图所示，则其外接球的体积为（　　）
A、9
2
π
B、
81
16
2
π
C、18π
D、6π
考点：球的体积和表面积,简单空间图形的三视图
专题：计算题,空间位置关系与距离
分析：由题意，正三棱锥的高为2
2
，底面三角形的高为3，设外接球的半径为R，则R2=（2
2
-R）2+（
2
3
×3）2，求出R，再求出正三棱锥的外接球的体积．
解答： 解：由题意，正三棱锥的高为2
2
，底面三角形的高为3，
设外接球的半径为R，则R2=（2
2
-R）2+（
2
3
×3）2，
∴R=
3
2
，
∴外接球的体积为
4
3
π•(
3
2
)3=9
2
π，
故选：A．
点评：本题考查外接球的体积，考查三视图，确定外接球的半径是关键．
练习册系列答案
相关题目
f（x）为R上的偶函数，若对任意的x1、x2∈（-∞，0]（x1≠x2），都有
f(x2)-f(x1)
x2-x1
＞0，则（　　）
A、f（-2）＜f（1）＜f（3）
B、f（1）＜f（-2）＜f（3）
C、f（3）＜f（-2）＜f（1）
D、f（3）＜f（1）＜f（-2）
若双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的离心率为
3
，则椭圆
x2
a2
+
y2
b2
=1的离心率为（　　）
A、
1
2
B、
3
3
C、
2
2
D、
3
2
已知数列{an}满足a1=1，
nan-an+1
an+1
=n，n∈N．
（1）求数列{an}的通项公式；
（2）设bn=
2n
an
，数列{bn}的前n项和为Tn，求Tn．
用数学归纳法证明“1+a+a2+…+an+1=
1-an+2
1-a
，(a≠1，n∈N*)”时，在验证n=1成立时，左边应该是（　　）
A、1+a+a2
B、1+a+a2+a3
C、1+a
D、1
已知椭圆C的中心在坐标原点，右焦点为F（1，0），A、B是椭圆C的左、右顶点，D是椭圆C上异于A、B的动点，且△ADB面积的最大值为
2
．
（1）求椭圆C的方程；
（2）是否存在一定点E（x0，0）（0＜x0＜
2
），使得当过点E的直线l与曲线C相交于A，B两点时，
1
|
EA
|2
+
1
|
EB
|2
为定值？若存在，求出定点和定值；若不存在，请说明理由．
一条光线从原点（0，0）射到直线l：2x-y+5=0上，再经反射后过B（1，3），求反射光线所在直线的方程．
在如图所示的茎叶图中，乙组数据的中位数是（　　）
A、84B、85C、86D、87
已知
a
=(1，1)，
b
=(x，0)，
c
=(2，4)，且(
a
+
b
)∥
c
，则实数x的值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网