题目内容
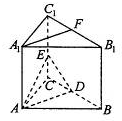 如图,在直三棱柱ABC-A1B1C1中,AB=AC,D、E分别是棱BC、CC1上的点(点D不在BC的端点处),且AD⊥DE,F为B1C1的中点.
如图,在直三棱柱ABC-A1B1C1中,AB=AC,D、E分别是棱BC、CC1上的点(点D不在BC的端点处),且AD⊥DE,F为B1C1的中点.(Ⅰ)求证:平面ADE⊥平面B1BCC1;
(Ⅱ)求证:A1F∥平面ADE.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:(Ⅰ)先证明AD⊥平面B1BCC1,然后,得到平面和平面垂直;(Ⅱ)首先,根据(Ⅰ)得AD⊥平面B1BCC1,连接DF,得DF∥AA1,且DF=AA1,即可得到相应的结论.
解答:
 解:(Ⅰ)证明:在直三棱柱ABC-A1B1C1中,CC1⊥平面ABC,AD平面ABC,∴AD⊥CC1,∵AD⊥DE,且DE∩CC1=D,
解:(Ⅰ)证明:在直三棱柱ABC-A1B1C1中,CC1⊥平面ABC,AD平面ABC,∴AD⊥CC1,∵AD⊥DE,且DE∩CC1=D,
∴AD⊥平面B1BCC1,
∵AD?平面ADE,∴平面ADE⊥平面B1BCC1,
(Ⅱ)根据(Ⅰ)得AD⊥平面B1BCC1,∵BC?平面B1BCC1,
∴AD⊥BC,
在△ABC中,AB=AC,∴D为BC的中点,
连接DF,得DF∥AA1,且DF=AA1,即四边形AA1FD为平行四边形,∴A1F∥AD,
∵AD?平面ADE,A1F?平面ADE,
A1F∥平面ADE.
 解:(Ⅰ)证明:在直三棱柱ABC-A1B1C1中,CC1⊥平面ABC,AD平面ABC,∴AD⊥CC1,∵AD⊥DE,且DE∩CC1=D,
解:(Ⅰ)证明:在直三棱柱ABC-A1B1C1中,CC1⊥平面ABC,AD平面ABC,∴AD⊥CC1,∵AD⊥DE,且DE∩CC1=D,∴AD⊥平面B1BCC1,
∵AD?平面ADE,∴平面ADE⊥平面B1BCC1,
(Ⅱ)根据(Ⅰ)得AD⊥平面B1BCC1,∵BC?平面B1BCC1,
∴AD⊥BC,
在△ABC中,AB=AC,∴D为BC的中点,
连接DF,得DF∥AA1,且DF=AA1,即四边形AA1FD为平行四边形,∴A1F∥AD,
∵AD?平面ADE,A1F?平面ADE,
A1F∥平面ADE.
点评:本题重点考查了空间中直线与平面平行、垂直,直线与直线平行的判定等知识,属于中档题,难度中等,解题关键是准确判断平行和垂直的判定和性质.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
如图是一个几何体的三视图,若该几何体的体积为
,则主视图中三角形的高x的值为( )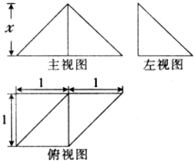
| 3 |
| 8 |

A、
| ||
B、
| ||
| C、1 | ||
D、
|