题目内容
用定义判断函数y=x3+
的奇偶性.
| 1 |
| x |
考点:函数奇偶性的判断
专题:函数的性质及应用
分析:根据函数奇偶性的定义即可得到结论.
解答:
解:函数f(x)的定义域为{x|x≠0},
则f(-x)=-x3-
=-(x3+
)=-f(x),
则函数f(x)是奇函数.
则f(-x)=-x3-
| 1 |
| x |
| 1 |
| x |
则函数f(x)是奇函数.
点评:本题主要考查函数奇偶性的判断,根据函数奇偶性的定义结合函数定义域的特点是解决本题的关键.

练习册系列答案
相关题目
如果f(x)为偶函数,满足在区间[2,3]上是增函数且最小值是4,那么f(x)在区间[-3,-2]上是( )
| A、增函数且最小值是-4 |
| B、增函数且最大值是4 |
| C、减函数且最小值是4 |
| D、减函数且最大值是-4 |
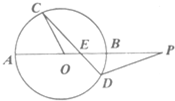 如图;圆O的割线PA过圆心O交圆于另一点B,弦CD交OB于点E,且△COE~△POE,PB=OA=2,则PE的长等于( )
如图;圆O的割线PA过圆心O交圆于另一点B,弦CD交OB于点E,且△COE~△POE,PB=OA=2,则PE的长等于( )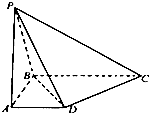 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠ABC=90°,AD∥BC,AD=1,BC=2,又PB=1,∠PBC=120°,AB⊥PC,直线AB与直线PD所成的角为60°.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠ABC=90°,AD∥BC,AD=1,BC=2,又PB=1,∠PBC=120°,AB⊥PC,直线AB与直线PD所成的角为60°.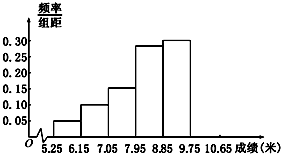 某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.
某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.