题目内容
已知f（t）=
，g（t）=
，求证：f（t）-g（t）=-2g（t2）．
| t |
| 1+t |
| t |
| 1-t |
考点：函数的值
专题：证明题,函数的性质及应用
分析：由f（t）、g（t），计算f（t）-g（t）与g（t2），即得结论．
解答：
证明：∵f（t）=
，g（t）=
，
∴f（t）-g（t）=
-
=
=
=-2g（t2）．
| t |
| 1+t |
| t |
| 1-t |
∴f（t）-g（t）=
| t |
| 1+t |
| t |
| 1-t |
=
| t(1-t)-t(1+t) |
| (1+t)(1-t) |
=
| -2t2 |
| 1-t2 |
=-2g（t2）．
点评：本题考查了利用函数的值证明等式成立的问题，也是一个求函数值的问题，是基础题．
练习册系列答案
冲刺100分单元优化练考卷系列答案
相关题目
已知△ABC中，a=4，b=4
，∠A=30°，则sinB等于（ ）
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
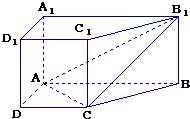直棱柱ABCD-A1B1C1D1中，底面ABCD是直角梯形，∠BAD=∠ADC=90°，AB=2AD=2CD=2．
如图，在四棱锥S-ABCD中，平面SAD⊥平面ABCD，四边形ABCD为正方形，且P为AD的中点，Q为SB的中点，M为BC的中点．