题目内容
现有5个质地,大小完全相同的小球上分别标有数字-1,-2,1,2,3,先将标有数字-2,1,3的小球放在第一个不透明的盒子里,再将其余小球放在第二个不透明的盒子里,现分别从这两个盒子里各随机取出一个小球.
(Ⅰ)请写出取出的两个小球上的数字之和所有可能的结果;
(Ⅱ)求取出两个小球上的数字之和等于0的概率.
(Ⅰ)请写出取出的两个小球上的数字之和所有可能的结果;
(Ⅱ)求取出两个小球上的数字之和等于0的概率.
考点:古典概型及其概率计算公式
专题:应用题,概率与统计
分析:(Ⅰ)利用列表法即可表示取出的两小球上的数字之和所有可能结果;
(Ⅱ)根据古典概型概率计算公式可求;
(Ⅱ)根据古典概型概率计算公式可求;
解答:
解:(Ⅰ)利用列表的方法表示取出的两个小球上的数字之和所有可能的结果是:
(Ⅱ)由(1)可知所有可能出现的结果有6种,所取两个数字和为0的有2种情况,
∴取出两个小球上的数字之和等于0的概率是:P=
=
.
| 第一个盒子 | -2 | -2 | 1 | 1 | 3 | 3 |
| 第二个盒子 | -1 | 2 | -1 | 2 | -1 | 2 |
| 取出的两数和 | -3 | 0 | 0 | 3 | 2 | 5 |
∴取出两个小球上的数字之和等于0的概率是:P=
| 2 |
| 6 |
| 1 |
| 3 |
点评:该题考查古典概型及其概率计算公式,属基础题.正确理解题意并能准确利用公式是解题关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
已知圆C1:(x+3)2+y2=1和圆C2:(x-3)2+y2=9,动圆M同时与圆C1及圆C2相外切,则动圆圆心M的轨迹方程是( )
A、x2-
| ||||
B、
| ||||
C、x2+
| ||||
D、
|
 某市为了配合宣传新《道路交通法》举办有奖征答活动,随机对该市15~65岁的人群抽样了n人,回答问题统计结果如图表所示.(如图是样本频率分布直方图,表是对样本中回答正确人数的分析统计表).
某市为了配合宣传新《道路交通法》举办有奖征答活动,随机对该市15~65岁的人群抽样了n人,回答问题统计结果如图表所示.(如图是样本频率分布直方图,表是对样本中回答正确人数的分析统计表).

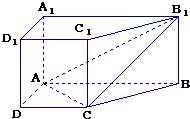 直棱柱ABCD-A1B1C1D1中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,AB=2AD=2CD=2.
直棱柱ABCD-A1B1C1D1中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,AB=2AD=2CD=2. 如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD,四边形ABCD为正方形,且P为AD的中点,Q为SB的中点,M为BC的中点.
如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD,四边形ABCD为正方形,且P为AD的中点,Q为SB的中点,M为BC的中点.