题目内容
 一同学为研究函数f(x)=
一同学为研究函数f(x)=| 1+x2 |
| 1+(1-x)2 |
| A、1 | B、2 | C、3 | D、4 |
考点:函数模型的选择与应用
专题:计算题
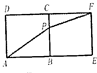
分析:把函数f(x)=
+
看作是图中的AP+PF,通过分析点P的特殊位置得到AP+PF的范围,而函数g(x)=4f(x)-9的零点的个数就是方程f(x)=
的解的个数,由
大于AP+PF的最小值且小于AP+PF的最大值可知f(x)=
的解有2个,则答案可求.
| 1+x2 |
| 1+(1-x)2 |
| 9 |
| 4 |
| 9 |
| 4 |
| 9 |
| 4 |
解答:
解:由题意可得:
函数f(x)=
+
=AP+PF,
当A、P、F共线时,f(x)取得最小值为
<
,
当P与B或C重合时,f(x)取得最大值为
+1>
.
g(x)=4f(x)-9=0,即f(x)=
.
故函数g(x)=4f(x)-9的零点的个数就是f(x)=
的解的个数.
而由题意可得f(x)=
的解有2个,
故选:B.
函数f(x)=
| 1+x2 |
| 1+(1-x)2 |
当A、P、F共线时,f(x)取得最小值为
| 5 |
| 9 |
| 4 |
当P与B或C重合时,f(x)取得最大值为
| 2 |
| 9 |
| 4 |
g(x)=4f(x)-9=0,即f(x)=
| 9 |
| 4 |
故函数g(x)=4f(x)-9的零点的个数就是f(x)=
| 9 |
| 4 |
而由题意可得f(x)=
| 9 |
| 4 |
故选:B.
点评:本题考查函数模型的选择及应用,考查数学转化思想方法,解答此题的关键是正确理解题意,是中档题.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
在△ABC中,内角A,B,C的对边分别为a,b,c,若sin2B-sin2C=
sinCsinA,a=2
c,则B=( )
| 3 |
| 3 |
| A、30° | B、60° |
| C、120° | D、150° |
 某同学在电脑上打下了一串黑白圆,如图所示,按这种规律往下排,那么第36个圆的颜色应是( )
某同学在电脑上打下了一串黑白圆,如图所示,按这种规律往下排,那么第36个圆的颜色应是( )| A、黑色 | B、白色 |
| C、白色可能性大 | D、黑色可能性大 |
已知集合A={-2,-1,1,2},B={x|x2-x-2≥0},则A∩(∁RB)=( )
| A、{1} |
| B、{-1,1} |
| C、{-2,1,2} |
| D、{-2,-1,1} |
首项为1,公差不为0的等差数列{an}中,a3、a4、a6是一个等比数列的前三项,则这个等比数列的第四项是( )
| A、8 | B、-8 | C、-6 | D、不确定 |
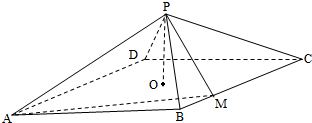 如图,四棱锥P-ABCD,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=
如图,四棱锥P-ABCD,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=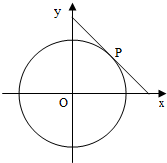 圆x2+y2=4的切线与x轴正半轴,y轴正半轴围成一个三角形,当该三角形面积最小时,切点为P(如图).
圆x2+y2=4的切线与x轴正半轴,y轴正半轴围成一个三角形,当该三角形面积最小时,切点为P(如图).