题目内容
已知α是第三象限角,且f(α)=
.
(1)化简f(α);
(2)已知cos(
-α)=
,求f(α)的值.
sin(5π-a)•cos(a+
| ||||
sin(a-
|
(1)化简f(α);
(2)已知cos(
| 3π |
| 2 |
| 1 |
| 5 |
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:(1)由条件利用诱导公式、同角三角函数的基本关系,化简可得所给式子的值,可得结果.
(2)由条件利用诱导公式求得sinα=-
,由此可得f(α)=sinα-
的值.
(2)由条件利用诱导公式求得sinα=-
| 1 |
| 5 |
| 1 |
| sinα |
解答:
解:(1)∵已知α是第三象限角,
∴f(α)=
=
=-
=
=sinα-
.
(2)∵cos(
-α)=-sinα=
,
∴sinα=-
,
∴f(α)=sinα-
=-
+5=
.
∴f(α)=
sin(5π-a)•cos(a+
| ||||
sin(a-
|
| sinα•(-sinα)(-cosα) |
| sinα•(-sinα)•tanα |
| cos2α |
| sinα |
| -(1-sin2α) |
| sinα |
=sinα-
| 1 |
| sinα |
(2)∵cos(
| 3π |
| 2 |
| 1 |
| 5 |
∴sinα=-
| 1 |
| 5 |
∴f(α)=sinα-
| 1 |
| sinα |
| 1 |
| 5 |
| 24 |
| 5 |
点评:本题主要考查同角三角函数的基本关系、诱导公式的应用,以及三角函数在各个象限中的符号,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
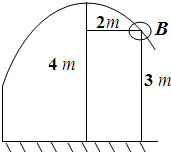 有一次姚明投篮时,测得投篮的轨迹是抛物线,如图所示,抛物线最高点离地面距离4m,篮筐B高为3m,篮筐中心离最高点的水平距离为2m,求投中时抛物线的方程?
有一次姚明投篮时,测得投篮的轨迹是抛物线,如图所示,抛物线最高点离地面距离4m,篮筐B高为3m,篮筐中心离最高点的水平距离为2m,求投中时抛物线的方程? △ABD,△BCF,△ACE分别是以△ABC三边AB,BC,AC做的等边三角形,连接BE,CD交于点G,连接FG,若BC=3,则线段FG长的最小值为
△ABD,△BCF,△ACE分别是以△ABC三边AB,BC,AC做的等边三角形,连接BE,CD交于点G,连接FG,若BC=3,则线段FG长的最小值为