题目内容
已知:等差数列{an}中,a4=14,前10项和S10=185.
(1)求an;
(2)数列{bn}满足bn=a2n求此数列的前n项和Gn.
(1)求an;
(2)数列{bn}满足bn=a2n求此数列的前n项和Gn.
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(1)根据a4=14,S10=185,列出方程,求出等差数列{an}的首项和公差,然后求出an即可;
(2)根据题意,首先求出数列{bn}的通项bn,然后根据等比数列的求和公式,求出此数列的前n项和Gn即可.
(2)根据题意,首先求出数列{bn}的通项bn,然后根据等比数列的求和公式,求出此数列的前n项和Gn即可.
解答:
解:(1)设等差数列{an}的公差为d,
∵
,
∴
,
解得
,
∴an=5+3(n-1)=3n+2,
即an=3n+2;
(2)根据bn=a2n,可得bn=3•2n+2,
=3•2n+1+2n-6(n∈N*),
即Gn=3•2n+1+2n-6,(n∈N*).
∵
|
∴
|
解得
|
∴an=5+3(n-1)=3n+2,
即an=3n+2;
(2)根据bn=a2n,可得bn=3•2n+2,
|
=3•2n+1+2n-6(n∈N*),
即Gn=3•2n+1+2n-6,(n∈N*).
点评:本题主要考查了等差数列的通项公式、前n项和公式,等比数列的前n项和公式的运用,属于中档题.

练习册系列答案
相关题目

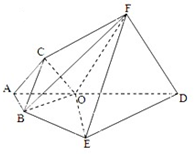 如图,ABEDFC为多面体,平面ABED与平面ACFD垂直,点O在线段AD上,OA=1,OD=2,△OAB,△OAC,△ODF,△ODE都是正三角形.
如图,ABEDFC为多面体,平面ABED与平面ACFD垂直,点O在线段AD上,OA=1,OD=2,△OAB,△OAC,△ODF,△ODE都是正三角形.