题目内容
15.已知表面积为24π的球外接于三棱锥S-ABC,且∠BAC=$\frac{π}{3}$,BC=4,则三棱锥S-ABC的体积最大值为( )| A. | $\frac{8\sqrt{2}}{3}$ | B. | $\frac{16\sqrt{2}}{3}$ | C. | $\frac{16}{3}$ | D. | $\frac{32}{3}$ |
分析 设球的半径为R,球心为O,如图所示,由球O的表面积是24π,可得4πR2=24π,解得R.设△ABC的外心为O1,外接圆的半径为r,则O1B=r=$\frac{1}{2}×\frac{4}{sin\frac{π}{3}}$=$\frac{4}{\sqrt{3}}$可得OO1=$\sqrt{O{B}^{2}-{O}_{1}{B}^{2}}$=$\frac{\sqrt{6}}{3}$,O1S=$\frac{4\sqrt{6}}{3}$.在△ABC中,由余弦定理可得:16=b2+c2-2bccos$\frac{π}{3}$,利用基本不等式的性质可得bc≤16,利用三棱锥P-ABC的体积V=$\frac{1}{3}×\frac{1}{2}bcsin\frac{π}{3}×\frac{4\sqrt{6}}{3}$,即可得出.
解答 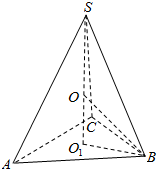 解:设球的半径为R,球心为O,如图所示
解:设球的半径为R,球心为O,如图所示
∵球O的表面积是24π,∴4πR2=24π,解得R=$\sqrt{6}$.
设△ABC的外心为O1,外接圆的半径为r,则O1B=r=$\frac{1}{2}×\frac{4}{sin\frac{π}{3}}$=$\frac{4}{\sqrt{3}}$,
∴OO1=$\sqrt{O{B}^{2}-{O}_{1}{B}^{2}}$=$\frac{\sqrt{6}}{3}$.
∴O1S=$\frac{4\sqrt{6}}{3}$.
在△ABC中,由余弦定理可得:16=b2+c2-2bccos$\frac{π}{3}$,
化为b2+c2=bc+16≥2bc,∴bc≤16,当且仅当b=c=4时取等号.
∴三棱锥S-ABC的体积V=$\frac{1}{3}×\frac{1}{2}bcsin\frac{π}{3}×\frac{4\sqrt{6}}{3}$≤$\frac{2\sqrt{6}}{9}×\frac{\sqrt{3}}{2}×16$=$\frac{16\sqrt{2}}{3}$,
故选:B.
点评 本题考查了三棱锥外接球的性质、勾股定理、三棱锥的体积计算公式、正弦定理余弦定理、基本不等式的性质,考查了推理能力与计算能力,属于中档题.

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案| A. | 若命题p:?x0∈R,x${\;}_{0}^{2}$-x0+1<0,则¬p:?x∉R,x2-x+1≥0 | |
| B. | 命题“若x=y,则cosx=cosy”的逆否命题为真命题 | |
| C. | 已知相关变量(x,y)满足线性回归方程$\widehat{y}$=2-3x,若变量x增加一个单位,则y平均增加3个单位 | |
| D. | 已知随机变量X~N(2,σ2),若P(X<a)=0.32,则P(X>4-a)=0.68 |
| A. | 0.648 | B. | 0.625 | C. | 0.375 | D. | 0.5 |
| 日期 | 7月15日 | 8月15日 | 9月15日 | 10月15日 | 11月15日 | 12月15日 |
| 摄氏温度x(℃) | 36 | 35 | 30 | 24 | 18 | 8 |
| 饮料杯数y | 27 | 29 | 24 | 18 | 15 | 5 |
(1)求选取2组数据恰好是相邻两个月的概率;
(2)若选中的是8月与12月的两组数据,根据剩下的4组数据,求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$;
(3)若由线性回归方程得到的估计数据与所选出的检验数据误差不超过3杯,则认为得到的线性回归方程是理想的,请问(2)所得到的线性回归方程是否理想.
附:对于一组数据(x1,y1),(x2,y2),…,(xn,yn),其回归直线y=bx+a的斜率和截距的最小二乘估计分别为$\widehat{b}$=$\frac{\sum_{i=1}^{n})({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$$\overline{x}$.