题目内容
5．已知π＜α＜$\frac{3}{2}$π，且sin2α=$\frac{4}{5}$，则sinα+cosα的值等于-$\frac{3\sqrt{5}}{5}$．分析 判断三角函数的符号，利用同角的关系式以及倍角公式进行求解即可．
解答 解：∵π＜α＜$\frac{3}{2}$π，
∴sinα＜0，cosα＜0，
即sinα+cosα＜0，
则sinα+cosα=-$\sqrt{（sinα+cosα）^{2}}$=-$\sqrt{1+sin2α}$=-$\sqrt{1+\frac{4}{5}}$=-$\sqrt{\frac{9}{5}}$=-$\frac{3\sqrt{5}}{5}$，
故答案为：-$\frac{3\sqrt{5}}{5}$．
点评 本题主要考查三角函数值的求解，利用条件判断三角函数的符号以及同角的关系式进行转化是解决本题的关键．
练习册系列答案
相关题目
20．已知函数f（x）=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}x（0＜x＜2）}\\{-{x}^{2}+8x-15（x≥2）}\end{array}\right.$，g（x）=kx-2，若方程f（x）=g（x）有三个根，则实数k的取值范围是（ ）
| A． | （0，$\frac{1}{2}$） | B． | （$\frac{1}{2}$，1） | C． | （-2$\sqrt{13}$+8，1） | D． | （$\frac{1}{2}$，-2$\sqrt{13}$+8） |
14．
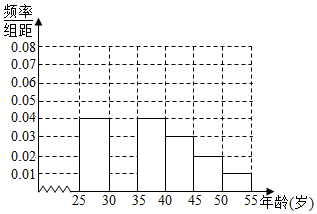某校学生利用元旦节进行社会实践，在[25，55]岁的人群随机抽取n人，进行了一次“是否已养成垃圾分类习惯”的调查，得到如下统计表和各年龄段人数频率分布直方图：
（Ⅰ）补全频率分布直方图并求n、a、p的值；
（Ⅱ）从[40，50）岁年龄段的“已养成垃圾分类习惯的人”中采用分层抽样法抽取6人参加垃圾分类宣讲活动，其中选取2人作为领队，求选取的2名领队年龄都在[40，45）岁的概率．
某校学生利用元旦节进行社会实践，在[25，55]岁的人群随机抽取n人，进行了一次“是否已养成垃圾分类习惯”的调查，得到如下统计表和各年龄段人数频率分布直方图：| 组数 | 分组 | 已养成垃圾分类习惯的人数 | 占本组频率 |
| 第一组 | [25，30） | 120 | 0.6 |
| 第二组 | [30，35） | 195 | p |
| 第三组 | [35，40） | 100 | 0.5 |
| 第四组 | [40，45） | a | 0.4 |
| 第五组 | [45，50） | 30 | 0.3 |
| 第六祖 | [50，55] | 15 | 0.3 |
（Ⅱ）从[40，50）岁年龄段的“已养成垃圾分类习惯的人”中采用分层抽样法抽取6人参加垃圾分类宣讲活动，其中选取2人作为领队，求选取的2名领队年龄都在[40，45）岁的概率．
15．已知表面积为24π的球外接于三棱锥S-ABC，且∠BAC=$\frac{π}{3}$，BC=4，则三棱锥S-ABC的体积最大值为（ ）
| A． | $\frac{8\sqrt{2}}{3}$ | B． | $\frac{16\sqrt{2}}{3}$ | C． | $\frac{16}{3}$ | D． | $\frac{32}{3}$ |