题目内容
7．某几何体的三视图如图所示，则该几何体的表面积为$4+4\sqrt{3}$．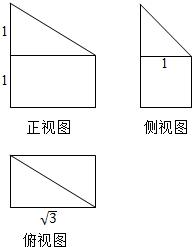
分析 判断几何体的形状，画出几何体的图形，利用三视图的数据求解几何体的表面积即可．
解答 解：由三视图可知，该几何体的直观图为三棱锥与长方体的组合体，其直观图如下：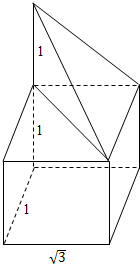
其中，三棱锥的底面是直角边长分别为$\sqrt{3}，1$的直角三角形，且有一条长为1的侧棱垂直于底面；
长方体的长、宽、高分别为$\sqrt{3}，1，1$，故该几何体的表面积为$S=1×1×2+\sqrt{3}×1×3+\frac{1}{2}×1×\sqrt{3}×2+\frac{1}{2}×1×2×2=4+4\sqrt{3}$．
故答案为：$4+4\sqrt{3}$．
点评 本题考查几何体的表面积的求法，考查画图能力以及空间想象能力，是中档题．
练习册系列答案
特高级教师点拨系列答案
相关题目
2．椭圆$\frac{x^2}{3}+\frac{y^2}{2}=1$的焦点坐标是（ ）
| A． | （0，±1） | B． | （±1，0） | C． | $（0，±\sqrt{2}）$ | D． | $（±\sqrt{2}，0）$ |
如图，四边形ABCD为等腰梯形，PD⊥平面ABCD，F为PC的中点，CD=AD=PD，AB=4AE=2CD=4．