Question

16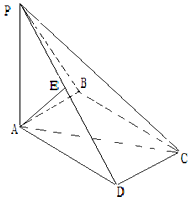．如图，在四棱锥P-ABCD中，PA⊥平面ABCD，∠ABC=90°，四边形ABCD是平行四边形，且PA=AD=2，AB=1，E是线段PD的中点．
（ 1 ） 求证：AE⊥PC；
（2）是否存在正实数λ，满足$\overrightarrow{PM}=λ\overrightarrow{MC}$，使得二面角M-BD-C的大小为60⁰？若存在，求出λ的值；若不存在，请说明理由．

Answer 1

分析 （1）证明PA⊥CD，CD⊥AD，即可证明CD⊥平面PAD，推出AE⊥CD，AE⊥PD，说明AE⊥平面PCD，然后证明AE⊥PC．
（2）建立空间直角坐标系，求出相关点的坐标，平面BCD的法向量，平面MBD的法向量，利用空间向量的数量积求解即可．

解答 （1）证明：∵∠ABC=90°，四边形ABCD是平行四边形∴四边形ABCD是矩形．∵PA⊥平面ABCD，∴PA⊥CD，又CD⊥AD，PA?平面PAD，AD?平面PAD∴CD⊥平面PAD，∵AE?平面PAD，∴AE⊥CD
又E是线段PD的中点，PA=AD，∴AE⊥PD，PD∩CD=D，∴AE⊥平面PCD，∵PC?平面PCD，∴AE⊥PC．…（5分）
（2）建立如图所示空间直角坐标系，A（0，0，0），D（2，0，0），B（0，1，0），P（0，0，2），C（2，1，0）…（7分）
由$\overrightarrow{PM}=λ\overrightarrow{MC}，（λ＞0）$，得$M（\frac{2λ}{1+λ}，\frac{λ}{1+λ}，\frac{2}{1+λ}）$…..（8分）
平面BCD的法向量$\overrightarrow m=（{0，0，1}）$…（9分）
设平面MBD的法向量$\overrightarrow n=（{x，y，z}）$，则$\overrightarrow{BD}=（{2，-1，0}）$，$\overrightarrow{DM}=（{-\frac{2}{1+λ}，\frac{λ}{1+λ}，\frac{2}{1+λ}}）$，
可解得$\overrightarrow n=（{1，2，1-λ}）$…（11分）
$|{cos\left?{\overrightarrow m，\overrightarrow n}\right＞}|=|{\frac{\overrightarrow m•\overrightarrow n}{{|{\overrightarrow m}|•|{\overrightarrow n}|}}}|=\frac{1}{2}$，∴$λ=\frac{{\sqrt{15}}}{3}+1$
故存在实数$λ=\frac{{\sqrt{15}}}{3}+1$，使得二面角M-BD-C的大小为60⁰…（12分）

点评 本题考查二面角的平面角的求法，最小与平面垂直的判定定理以及性质定理的应用，考查空间想象能力以及计算能力．