题目内容
5.经过圆x2+2x+y2=0的圆心,且与直线x+y-2=0垂直的直线方程是x-y+1=0.分析 化圆的方程为标准方程,求出圆心坐标,再由已知可得所求直线的斜率,代入直线方程的点斜式得答案.
解答 解:化圆x2+2x+y2=0为标准方程(x+1)2+y2=1,
可得圆心坐标为(-1,0).
∵直线x+y-2=0的斜率为-1,
∴与直线x+y-2=0垂直的直线的斜率为1.
则所求直线方程为y-0=1×(x+1),即x-y+1=0.
故答案为:x-y+1=0.
点评 本题考查直线与圆的位置关系的应用,考查两直线垂直与斜率的关系,是基础题.

练习册系列答案
相关题目
16.设等差数列{an}的前n项和为Sn,$\overrightarrow{a}$=(a1,1),$\overrightarrow{b}$=(1,a10),若$\overrightarrow{a}$•$\overrightarrow{b}$=20,且S11=121,bn=$\frac{1}{{a}_{n}{a}_{n+1}}$+$\frac{1}{\sqrt{{a}_{n}}+\sqrt{{a}_{n+1}}}$,则数列{bn}的前40项和为( )
| A. | $\frac{72.8}{81}$ | B. | $\frac{182}{81}$ | C. | $\frac{364}{81}$ | D. | $\frac{91}{81}$ |
14.设A(0,1),B(1,3),C(-1,5),D(0,-1),则$\overrightarrow{AB}+\overrightarrow{AC}$等于( )
| A. | -2$\overrightarrow{AD}$ | B. | 2$\overrightarrow{AD}$ | C. | -3$\overrightarrow{AD}$ | D. | 3$\overrightarrow{AD}$ |
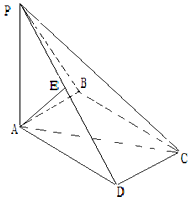 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=90°,四边形ABCD是平行四边形,且PA=AD=2,AB=1,E是线段PD的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=90°,四边形ABCD是平行四边形,且PA=AD=2,AB=1,E是线段PD的中点.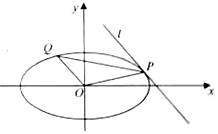 如图,P(x0,y0)是椭圆$\frac{{x}^{2}}{3}$+y2=1的上的点,l是椭圆在点P处的切线,O是坐标原点,OQ∥l与椭圆的一个交点是Q,P,Q都在x轴上方
如图,P(x0,y0)是椭圆$\frac{{x}^{2}}{3}$+y2=1的上的点,l是椭圆在点P处的切线,O是坐标原点,OQ∥l与椭圆的一个交点是Q,P,Q都在x轴上方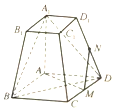 如图,在四棱台ABCD-A1B1C1D1中,底面ABCD为平行四边形,∠BAD=120°,M为CD上的点.且∠A1AB=∠A1AD=90°,AD=A1A=2,A1B1=DM=1.
如图,在四棱台ABCD-A1B1C1D1中,底面ABCD为平行四边形,∠BAD=120°,M为CD上的点.且∠A1AB=∠A1AD=90°,AD=A1A=2,A1B1=DM=1.