题目内容
4.已知抛物线的顶点在坐标原点,对称轴是x轴,顶点与焦点的距离等于4.(1)求抛物线的方程
(2)若等边三角形的一个顶点位于原点,另外两个顶点在抛物线上,求这个等边三角形的边长.
分析 (1)设抛物线方程为y2=±2px(p>0),由题意可得$\frac{p}{2}=4,p=8$,可得抛物线的方程;
(2)不妨以抛物线y2=16x进行计算.
根据抛物线的对称性可得∠AOx=30°,可设直线OA的方程为$y=\frac{\sqrt{3}}{3}x$
由$\left\{\begin{array}{l}{y=\frac{\sqrt{3}}{3}x}\\{{y}^{2}=16x}\end{array}\right.$得A(48,16$\sqrt{3}$),B(48,-16$\sqrt{3}$).
即等边三角形AOB的边长为AB=32$\sqrt{3}$
解答 解:(1)设抛物线方程为y2=±2px(p>0),由题意可得$\frac{p}{2}=4,p=8$
∴抛物线的方程为y2=±16x;
(2)不妨以抛物线y2=16x进行计算.
∵等边三角形的一个顶点位于原点,另外两个顶点在抛物线上,∴根据抛物线的对称性可得(如图)
∠AOx=30°,可设直线OA的方程为$y=\frac{\sqrt{3}}{3}x$
由$\left\{\begin{array}{l}{y=\frac{\sqrt{3}}{3}x}\\{{y}^{2}=16x}\end{array}\right.$得A(48,16$\sqrt{3}$)
根据对称性得B(48,-16$\sqrt{3}$).
∴AB=32$\sqrt{3}$,∴等边三角形AOB的边长为32$\sqrt{3}$.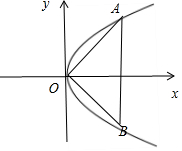
点评 本题考查了抛物线的方程、性质,直线与抛物线的位置关系,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.设等差数列{an}的前n项和为Sn,$\overrightarrow{a}$=(a1,1),$\overrightarrow{b}$=(1,a10),若$\overrightarrow{a}$•$\overrightarrow{b}$=20,且S11=121,bn=$\frac{1}{{a}_{n}{a}_{n+1}}$+$\frac{1}{\sqrt{{a}_{n}}+\sqrt{{a}_{n+1}}}$,则数列{bn}的前40项和为( )
| A. | $\frac{72.8}{81}$ | B. | $\frac{182}{81}$ | C. | $\frac{364}{81}$ | D. | $\frac{91}{81}$ |
14.设A(0,1),B(1,3),C(-1,5),D(0,-1),则$\overrightarrow{AB}+\overrightarrow{AC}$等于( )
| A. | -2$\overrightarrow{AD}$ | B. | 2$\overrightarrow{AD}$ | C. | -3$\overrightarrow{AD}$ | D. | 3$\overrightarrow{AD}$ |
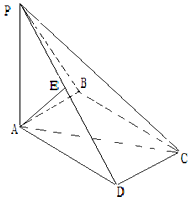 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=90°,四边形ABCD是平行四边形,且PA=AD=2,AB=1,E是线段PD的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=90°,四边形ABCD是平行四边形,且PA=AD=2,AB=1,E是线段PD的中点.