题目内容

4．数列{an}的前n项和为Sn，满足a1=1，${2^{{a_{n+1}}}}=2•{4^{a_n}}$，则S5的值为（　　）
A．57B．58C．62D．63

分析 由${2^{{a_{n+1}}}}=2•{4^{a_n}}$得${2^{{a_{n+1}}}}=2•{4^{a_n}}={2^{2{a_n}+1}}$，可得an+1=2an+1，变形为an+1+1=2（an+1）．利用等比数列的通项公式与求和公式即可得出．

解答 解：由${2^{{a_{n+1}}}}=2•{4^{a_n}}$得${2^{{a_{n+1}}}}=2•{4^{a_n}}={2^{2{a_n}+1}}$，
∴an+1=2an+1，∴an+1+1=2（an+1）．
∴{an+1}是以2为首项2为公比的等比数列，
∴${a_n}+1={2^n}$，∴${a_n}={2^n}-1$．
∴${S_5}=（{2+{2^2}+…+{2^5}}）-5=57$．
故选：A．

点评 本题考查了数列递推关系、等比数列的通项公式与求和公式，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
14．已知数列{an}和{bn}满足：${a_{n+k}}-{（{-1}）^k}•{a_n}={b_n}（n∈{N^*}）$．
（1）若$k=1，{a_1}=1，{b_n}={2^n}$，求数列{an}的通项公式；
（2）若k=4，bn=8，a1=4，a2=6，a3=8，a4=10．
①求证：数列{an}为等差数列；
②记数列{an}的前n项和为Sn，求满足${（{{S_n}+1}）^2}-\frac{3}{2}{a_n}+33={k^2}$的所有正整数k和n的值．
15．椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$过点P（$\sqrt{3}$，1）且离心率为$\frac{\sqrt{6}}{3}$，F为椭圆的右焦点，过F的直线交椭圆C于M，N两点，定点A（-4，0）．
（Ⅰ）求椭圆C的方程；
（Ⅱ）若△AMN面积为3$\sqrt{3}$，求直线MN的方程．
12．已知函数f（x）=sin（$\frac{x}{4}$-$\frac{π}{3}$），若存在实数x1，x2使得对任意实数x，都有f（x1）≤f（x）≤f（x2），则|x1-x2|的最小值是（　　）
A．8πB．4πC．2πD．π
19．设实数x，y满足约束条件$\left\{\begin{array}{l}x-y≥1\\ x+y≤4\\ x≥0\\ y≥0\end{array}\right.$，则目标函数z=x-3y的取值范围为（　　）
A．[-12，1]B．[-12，0]C．[-2，4]D．[1，4]
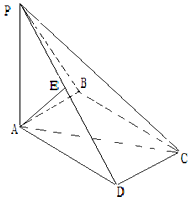9．从5名男公务员和4名女公务员中选出3人，分别派到西部的三个不同地区，要求3人中既有男公务员又有女公务员，则不同的选派方法种数是420．
16．如图，在四棱锥P-ABCD中，PA⊥平面ABCD，∠ABC=90°，四边形ABCD是平行四边形，且PA=AD=2，AB=1，E是线段PD的中点．
（ 1 ） 求证：AE⊥PC；
（2）是否存在正实数λ，满足$\overrightarrow{PM}=λ\overrightarrow{MC}$，使得二面角M-BD-C的大小为600？若存在，求出λ的值；若不存在，请说明理由．
12．化简：
（1）sin（-α）cos（-α-π）tan（2π+α）；
（2）$\frac{sin（180°+α）cos（-α）}{tan（-α）}$；
（3）$\frac{cos（α+π）sin（-α）}{cos（-3π-α）sin（-α-4π）}$；
（4）sin2（-α）+tan（2π+α）cos2（π+α）．
13．已知f（x）=lnx-ax+$\frac{1-a}{x}$-1（a∈R）．
（Ⅰ）当a=-1时，求曲线y=f（x）在（2，f（2））处的切线方程；
（Ⅱ）当0≤a≤$\frac{1}{2}$时，试讨论f（x）的单调性．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网