题目内容
17.设f(x)=x2+ax+2(a∈R),若{y|y=f(f(x))}={y|y=f(x)},则实数a的取值范围是(-∞,-2]∪[4,+∞).分析 由两函数值域相同可知f(x)的值域里含有元素-$\frac{a}{2}$,列出不等式解出a即可.
解答 解:f(x)=x2+ax+2=(x+$\frac{a}{2}$)2+2-$\frac{{a}^{2}}{4}$,
∴当x=-$\frac{a}{2}$时,f(x)取得最小值2-$\frac{{a}^{2}}{4}$.
∵f(f(x))的值域与f(x)的值域相同,
∴-$\frac{a}{2}$∈{y|y=f(x)},
即-$\frac{a}{2}$≥2-$\frac{{a}^{2}}{4}$,解得a≤-2或a≥4,
故答案为:(-∞,-2]∪[4,+∞).
点评 本题考查了二次函数的性质,不等式的解法,属于中档题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
8.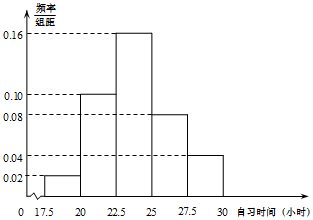 某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].则这200名学生中每周的自习时间不低于25小时的人数为( )
某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].则这200名学生中每周的自习时间不低于25小时的人数为( )
 某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].则这200名学生中每周的自习时间不低于25小时的人数为( )
某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].则这200名学生中每周的自习时间不低于25小时的人数为( )| A. | 30 | B. | 60 | C. | 80 | D. | 120 |
12.在二项式(x-2)5的展开式中,含x3项的系数为( )
| A. | -80 | B. | -40 | C. | 40 | D. | 80 |
9.设等差数列{an}的前n项和为Sn,若a4,a6是方程x2-18x+p=0的两根,那么S9=( )
| A. | 9 | B. | 81 | C. | 5 | D. | 45 |