Question

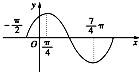函数f（x）=Asin（ωx+φ）的图象如图所示．试依图推出：
（1）f（x）的最小正周期；
（2）f（x）的单调递增区间；
（3）使f（x）取最小值的x的取值集合．

Answer 1

考点：正弦函数的图象

专题：三角函数的图像与性质

分析：（1）由图象可知，

T

2

=

3

2

π，故计算可得T=3π；
（2）由（1）可知当x=

7

4

π-3π=-

5

4

π时，函数f（x）取最小值，故计算可得f（x）的单调递增区间是[-

5π

4

+3kπ，

π

4

+3kπ]，(k∈Z)；
（3）由图知x=

7

4

π时，f（x）取最小值，又T=3π，故所以f（x）取最小值时x的集合为{x/x=

7π

4

+3kπ，k∈Z}．

解答： 解：（1）由图象可知，

T

2

=

7

4

π-

π

4

=

3

2

π，
∴T=3π．
（2）由（1）可知当x=

7

4

π-3π=-

5

4

π时，函数f（x）取最小值，
∴f（x）的单调递增区间是[-

5π

4

+3kπ，

π

4

+3kπ]，(k∈Z)
（3）由图知x=

7

4

π时，f（x）取最小值，
又∵T=3π，∴当x=

7

4

π+3kπ时，f（x）取最小值，
所以f（x）取最小值时x的集合为{x/x=

7π

4

+3kπ，k∈Z}．

点评：本题主要考察正弦函数的图象的性质，属于基础题．