题目内容
已知函数f(x)=ax-
-a+1,当a>0,求关于x的不等式f(x)<0的解集.
| 1 |
| x |
考点:其他不等式的解法
专题:分类讨论,不等式的解法及应用
分析:先求出f(x)的定义域是(-∞,0)∪(0,+∞),再讨论x>0时,x<0时,不等式f(x)<0的解集是什么.
解答:
解:∵f(x)=ax-
-a+1的定义域是(-∞,0)∪(0,+∞),
且f(x)<0,
即ax-
-a+1<0;
∴当x>0时,ax2-1-(a-1)x<0,
即(ax+1)(x-1)<0;
∵a>0,∴-
<1,
∴-
<x<1,
得不等式的解为0<x<1;
当x<0时,ax2-1-(a-1)x>0,
即(ax+1)(x-1)>0,
解得x<-
,或x>1,
得不等式的解为x<-
;
综上,f(x)<0的解集为(-∞,-
)∪(0,1).
| 1 |
| x |
且f(x)<0,
即ax-
| 1 |
| x |
∴当x>0时,ax2-1-(a-1)x<0,
即(ax+1)(x-1)<0;
∵a>0,∴-
| 1 |
| a |
∴-
| 1 |
| a |
得不等式的解为0<x<1;
当x<0时,ax2-1-(a-1)x>0,
即(ax+1)(x-1)>0,
解得x<-
| 1 |
| a |
得不等式的解为x<-
| 1 |
| a |
综上,f(x)<0的解集为(-∞,-
| 1 |
| a |
点评:本题考查了含有字母系数的不等式的解法与应用问题,解题时应用分类讨论思想,是中档题.

练习册系列答案
相关题目
若定义域为(0,3)的函数f(x)是增函数,且f(2a-1)<f(a),则a的取值范围是( )
| A、(-∞,1) | ||
| B、(0,1) | ||
C、(
| ||
| D、(1,3) |
已知非空集合M和N,规定M-N={x|x∈M且x∉N},那么M-(M-N)等于( )
| A、M∪N | B、M∩N | C、M | D、N |
将一个直角梯形绕其较短的底所在的直线旋转一周得到一个几何体,关于该几何体的以下描绘中,正确的是( )
| A、是一个圆台 |
| B、是一个圆柱 |
| C、是一个圆柱和一个圆锥的简单组合体 |
| D、是一个圆柱被挖去一个圆锥后所剩的几何体 |
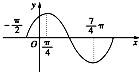 函数f(x)=Asin(ωx+φ)的图象如图所示.试依图推出:
函数f(x)=Asin(ωx+φ)的图象如图所示.试依图推出: