题目内容
函数y=
的单调减区间是 .
| x2-2x-8 |
考点:复合函数的单调性
专题:函数的性质及应用
分析:令t=x2-2x-8≥0,求得x的范围,可得函数的定义域,且y=
,本题即求函数t在函数y的定义域内的减区间.再利用二次函数的性质可得函数t在函数y的定义域内的减区间.
| t |
解答:
解:令t=x2-2x-8=(x-4)(x+2)≥0,求得x≤-2,或x≥4,故函数的定义域为(-∞,-2]∪[4,+∞),且y=
,
故本题即求函数t在函数y的定义域内的减区间.
再利用二次函数的性质可得函数t在函数y的定义域内的减区间为(-∞,-2],
故答案为:(-∞,-2].
| t |
故本题即求函数t在函数y的定义域内的减区间.
再利用二次函数的性质可得函数t在函数y的定义域内的减区间为(-∞,-2],
故答案为:(-∞,-2].
点评:本题主要考查复合函数的单调性,二次函数的性质,体现了转化的数学思想,属于基础题.

练习册系列答案
相关题目
从装有2个白球和2个蓝球的口袋中任取2个球,那么对立的两个事件是( )
| A、“恰有一个白球”与“恰有两个白球” |
| B、“至少有一个白球”与“至少有-个蓝球” |
| C、“至少有-个白球”与“都是蓝球” |
| D、“至少有一个白球”与“都是白球” |
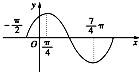 函数f(x)=Asin(ωx+φ)的图象如图所示.试依图推出:
函数f(x)=Asin(ωx+φ)的图象如图所示.试依图推出: