题目内容
已知cos(π+α)=-
,且α是第四象限角,则sin(-2π-α)= .
| 3 |
| 5 |
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:由条件利用诱导公式求得cosα=
,再由α是第四象限角,求得sinα的值,再利用诱导公式求得sin(-2π-α)的值.
| 3 |
| 5 |
解答:
解:∵cos(π+α)=-cosα=-
,∴cosα=
,又∵α是第四象限角,∴sinα=-
,
则sin(-2π-α)=sin(-α)=-sinα=
,
故答案为:
.
| 3 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
则sin(-2π-α)=sin(-α)=-sinα=
| 4 |
| 5 |
故答案为:
| 4 |
| 5 |
点评:本题主要考查同角三角函数的基本关系,诱导公式的应用,以及三角函数在各个象限中的符号,属于基础题.

练习册系列答案
相关题目
两个非零向量
,
垂直的充要条件是( )
| a |
| b |
A、|
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、(
|
已知命题p:实数x满足logax>loga(2-x),其中0<a<1,则使命题p成立的必要不充分条件是( )
| A、1<x<2 | ||
| B、0<x<1 | ||
| C、-1<x<1 | ||
D、
|
若
≠kx(k∈R)对于一切x∈[
,5]均成立,则有( )
| x-1 |
| 10 |
| 9 |
A、
| ||||
B、
| ||||
C、k<
| ||||
D、k<
|
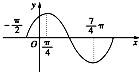 函数f(x)=Asin(ωx+φ)的图象如图所示.试依图推出:
函数f(x)=Asin(ωx+φ)的图象如图所示.试依图推出: