题目内容
已知函数f(x)=sin
,x∈R,将函数y=f(x)图象上所有点的横坐标缩短为原来的
倍(纵坐不变),得到函数g(x)的图象,则关于f(x)•g(x)有下列命题:
①函数y=f(x)•g(x)是奇函数;
②函数y=f(x)•g(x)不是周期函数;
③函数y=f(x)•g(x)的图象关于点(π,0)中心对称;
④函数y=f(x)•g(x)的最大值为
.
其中真命题为 .
| x |
| 2 |
| 1 |
| 2 |
①函数y=f(x)•g(x)是奇函数;
②函数y=f(x)•g(x)不是周期函数;
③函数y=f(x)•g(x)的图象关于点(π,0)中心对称;
④函数y=f(x)•g(x)的最大值为
| ||
| 3 |
其中真命题为
考点:命题的真假判断与应用
专题:函数的性质及应用
分析:本题可先根据图象平移的规律求出g(x)的解析式,再研究函数f(x)•g(x)的奇偶性、周期性、对称性和最值,从而选出正确选项.
解答:
解:∵函数f(x)=sin
,x∈R,
∴将函数y=f(x)图象上所有点的横坐标缩短为原来的
倍(纵坐不变),函数g(x)=sinx.
∴f(x)•g(x)=sinx•sin
.
记h(x)=sinx•sin
.
(1)h(-x)=sin(-x)•sin(-
)=(-sinx)•(-sin
)=sinx•sin
.
∴h(-x)=h(x).
∴h(x)是偶函数.
假设h(x)是奇函数,则h(x)=0恒成立,与h(x)=sinx•sin
矛盾.
故假设不成立.
∴h(x)不是奇函数.即①不成立.
(2)∵h(x+4π)=sin(x+4π)•sin
=sinx•sin(
+2π)=sinx•sin
=h(x),
∴h(x)是周期函数.故②不成立.
(3)设P(x,y)是函数y=h(x)图象上任意一点,
则 y=sinx•sin
.
点P(x,y)关于点(π,0)的对称点是P′(2π-x,-y),
∵sin(2π-x)•sin
=sinx•sin(π-
)=-sinx•sin
=-y
∴点是P′(2π-x,-y)也在函数 y=sinx•sin
的图象上.
∴函数y=f(x)•g(x)的图象关于点(π,0)中心对称.
∴③成立.
(4)h(x)=sinx•sin
=2sin2
•cos
.
令cos
=t,则sin2
=1-t2.
H(x)=2(1-t2)t=-2t3+2t,(-1≤t≤1)
H′(t)=-6t2+2=-6(t-
)(t+
).
当-1<x<-
时,H′(x)<0,H(x)单调递减;
当-
<x<
时,H′(x)>0,H(x)单调递增;
当
<x<1时,H′(x)<0,H(x)单调递减.
∵H(-1)=2-2=0,H(
)=
,
∴H(x)的最大值为
.
∴④不成立.
故答案为③.
| x |
| 2 |
∴将函数y=f(x)图象上所有点的横坐标缩短为原来的
| 1 |
| 2 |
∴f(x)•g(x)=sinx•sin
| x |
| 2 |
记h(x)=sinx•sin
| x |
| 2 |
(1)h(-x)=sin(-x)•sin(-
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
∴h(-x)=h(x).
∴h(x)是偶函数.
假设h(x)是奇函数,则h(x)=0恒成立,与h(x)=sinx•sin
| x |
| 2 |
故假设不成立.
∴h(x)不是奇函数.即①不成立.
(2)∵h(x+4π)=sin(x+4π)•sin
| x+4π |
| 2 |
| x |
| 2 |
| x |
| 2 |
∴h(x)是周期函数.故②不成立.
(3)设P(x,y)是函数y=h(x)图象上任意一点,
则 y=sinx•sin
| x |
| 2 |
点P(x,y)关于点(π,0)的对称点是P′(2π-x,-y),
∵sin(2π-x)•sin
| 2π-x |
| 2 |
| x |
| 2 |
| x |
| 2 |
∴点是P′(2π-x,-y)也在函数 y=sinx•sin
| x |
| 2 |
∴函数y=f(x)•g(x)的图象关于点(π,0)中心对称.
∴③成立.
(4)h(x)=sinx•sin
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
令cos
| x |
| 2 |
| x |
| 2 |
H(x)=2(1-t2)t=-2t3+2t,(-1≤t≤1)
H′(t)=-6t2+2=-6(t-
| ||
| 3 |
| ||
| 3 |
当-1<x<-
| ||
| 3 |
当-
| ||
| 3 |
| ||
| 3 |
当
| ||
| 3 |
∵H(-1)=2-2=0,H(
| ||
| 3 |
| 4 |
| 9 |
| 3 |
∴H(x)的最大值为
| 4 |
| 9 |
| 3 |
∴④不成立.
故答案为③.
点评:本题考查了函数的图象平移、函数的单调性、函数的奇偶性、函数的周期性、函数的最值,用到了换元法化简,导数法求最值.本题虽然是填空题,但计算量较大,思维要求高,属于中档题.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
函数f(x)=x3-3bx+3b在(0,1)内有极小值的充分不必要条件是( )
| A、b∈(0,1) | ||
| B、b∈(1,+∞) | ||
C、b∈(
| ||
| D、b∈(-∞,1) |
在等差数列{an}中,Sn表示前n项和,a1+a6=5,则S6=( )
| A、15 | B、18 | C、12 | D、16 |
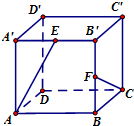 正方体ABCD-A′B′C′D′中,点E为A1B1的中点,F为B1B的中点,则AE与CF所成角的余弦值为
正方体ABCD-A′B′C′D′中,点E为A1B1的中点,F为B1B的中点,则AE与CF所成角的余弦值为