题目内容

在数列{an}中，a1=1，an+1-an=n（n∈N*），则a100的值为
 
．
考点：数列递推式
专题：点列、递归数列与数学归纳法
分析：由数列递推式结合已知求出数列的通项，则a100的值可求．
解答： 解：由an+1-an=n（n∈N*），得：
an=（an-an-1）+（an-1+an-2）+…+（a2-a1）+a1（n≥2），
则an=（n-1）+（n-2）+…+1+a1 
=
n(n-1)
2
+a1．
∵a1=1，
∴an=
n(n-1)
2
+1．
则a100=
100×99
2
+1=4951．
故答案为：4951．
点评：本题考查了数列递推式，考查了累加法求数列的通项公式，是中档题．
练习册系列答案
相关题目
下列说法中正确的是
 
．
①若散点图所有点都在一条直线附近，则这条直线为回归直线；
②已知随机变量?服从正态分布N（2，a2），且P（ξ＜4）=0.9，则P（0＜ξ＜2）=0.4；
③
∫
0
-1
1-x2
dx=
∫
1
0
1-x2
dx=
π
4
；
④E（2ξ+3）=2E（ξ+3）；D（2ξ+3）=2D（ξ）+3．
若关于x的方程sin2x+2sinx-1+m=0有解．则实数m的范围
 
．
已知函数f（x）=sin
x
2
，x∈R，将函数y=f（x）图象上所有点的横坐标缩短为原来的
1
2
倍（纵坐不变），得到函数g（x）的图象，则关于f（x）•g（x）有下列命题：
①函数y=f（x）•g（x）是奇函数；
②函数y=f（x）•g（x）不是周期函数；
③函数y=f（x）•g（x）的图象关于点（π，0）中心对称；
④函数y=f（x）•g（x）的最大值为
3
3
．
其中真命题为
 
．
A、B两盏路灯之间长度是30米，想在其间随意安两盏路灯C、D，A与C，B与D之间的距离都不小于10米的概率为
 
．
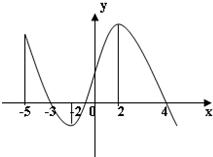如图所示是f′（x）的图象，则正确的判断个数是（　　）
（1）f（x）在（-5，-3）上是减函数；
（2）x=4是极大值点；
（3）x=2是极值点；
（4）f（x）在（-2，2）上先减后增．
A、0B、1C、2D、3
设m，n是两条不同的直线，α、β、γ是三个不同的平面，给出下列命题，正确的是（　　）
A、若m?β，α⊥β，则m⊥α
B、若m∥α，m⊥β，则α⊥β
C、若α⊥β，α⊥γ，则β⊥γ
D、若α∩γ=m，β∩γ=n，m∥n，则α∥β
已知函数f（x）=acos（πx+β）+bsin（πx+α），且f（2013）=6，则f（2014）的值是（　　）
A、-6B、-1C、-3D、6
在正方体中，直线A1B与B1C所成的角的大小为（　　）
A、30°B、45°
C、60°D、90°

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网