题目内容
数列{an}中,Sn是其前n项和,若a1=1,an+1=3Sn (n∈N*),则a4= .
考点:数列递推式,数列的函数特性
专题:等差数列与等比数列
分析:根据递推关系,求出数列{an}的通项公式,即可得到结论.
解答:
解:∵a1=1,an+1=3Sn (n∈N*),
∴an+2=3Sn+1 (n∈N*),
两式相减得an+2-an+1=3Sn+1-3Sn=3an+1.
即an+2=4an+1,
∵a1=1,an+1=3Sn,
∴a2=3S1=3,
a3=4a2=12,a4=4a3=4×12=48,
故答案为:48.
∴an+2=3Sn+1 (n∈N*),
两式相减得an+2-an+1=3Sn+1-3Sn=3an+1.
即an+2=4an+1,
∵a1=1,an+1=3Sn,
∴a2=3S1=3,
a3=4a2=12,a4=4a3=4×12=48,
故答案为:48.
点评:本题主要考查数列项的求解,根据数列的递推关系是解决本题的关键,考查学生的运算能力.

练习册系列答案
相关题目
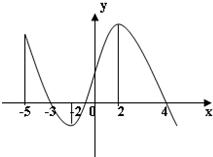 如图所示是f′(x)的图象,则正确的判断个数是( )
如图所示是f′(x)的图象,则正确的判断个数是( )(1)f(x)在(-5,-3)上是减函数;
(2)x=4是极大值点;
(3)x=2是极值点;
(4)f(x)在(-2,2)上先减后增.
| A、0 | B、1 | C、2 | D、3 |
函数f(x)=
-cosx在(0,+∞)内图象与X轴交点个数( )
| x |
| A、零个 | B、有且仅有一个 |
| C、有且仅有两个 | D、有无穷多个 |